2023年苏科版数学七年级下册全方位训练卷7.2探索平行线的性质
试卷更新日期:2023-02-07 类型:同步测试
一、单选题(每题3分,共24分)
-
1. 如图,直线 , 如果 , , 那么的度数是( )
 A、31° B、40° C、39° D、70°2. 如图,若 , , , 则的度数是( )
A、31° B、40° C、39° D、70°2. 如图,若 , , , 则的度数是( )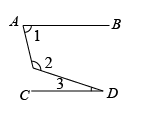 A、25° B、30° C、36° D、38°3. 如图,直线 , 直线与直线 , 分别交于点 , 点 , 于点 , 交直线于点 . 如果 , 那么的度数为( )
A、25° B、30° C、36° D、38°3. 如图,直线 , 直线与直线 , 分别交于点 , 点 , 于点 , 交直线于点 . 如果 , 那么的度数为( )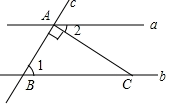 A、 B、 C、 D、4. 如图,将三角板的直角顶点放在两条平行线a,b中的直线b上,如果∠1=42°,则∠2的度数是( )
A、 B、 C、 D、4. 如图,将三角板的直角顶点放在两条平行线a,b中的直线b上,如果∠1=42°,则∠2的度数是( ) A、30° B、40° C、48° D、45°5. 如图,直线// , 则的度数是( )
A、30° B、40° C、48° D、45°5. 如图,直线// , 则的度数是( )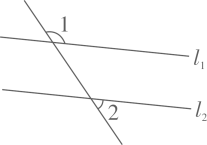 A、30° B、40° C、50° D、65°6. 如图,AB∥CD,直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为( )
A、30° B、40° C、50° D、65°6. 如图,AB∥CD,直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为( ) A、28° B、62° C、56° D、72°7. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的的度数是( )
A、28° B、62° C、56° D、72°7. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的的度数是( ) A、 B、 C、 D、8. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( )
A、 B、 C、 D、8. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共24分)
-
9. 如图,已知直线、被直线所截,且∥ , ∠1=°,那么∠2 =度;
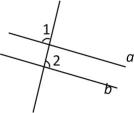 10. 如图, , 直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= .
10. 如图, , 直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= . 11. 如图,将一块含有角的直角三角板的两个顶点放在作业本两行线上.如果 , 那么的度数是 .
11. 如图,将一块含有角的直角三角板的两个顶点放在作业本两行线上.如果 , 那么的度数是 . 12. 如图,AB∥CD, , , , 平分 , 则°.
12. 如图,AB∥CD, , , , 平分 , 则°. 13. 把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则∠BGE= .
13. 把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则∠BGE= . 14. 如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=°.
14. 如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=°. 15. 如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3=°.
15. 如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3=°. 16. 如图,一幅三角板的两个直角顶点重合,已知 , , 则当的一边与的一边平行或重合,且点C在的左侧时,(小于平角)的度数为 .
16. 如图,一幅三角板的两个直角顶点重合,已知 , , 则当的一边与的一边平行或重合,且点C在的左侧时,(小于平角)的度数为 .
三、解答题(共10题,共102分)
-
17. 填空并完成以下证明:
如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.

解:∠AED与∠C的大小关系是 .
证明:∵∠1+∠2=180°(已知)
∠1=∠DFH( )
∴ =180°
∴EH∥AB( )
∴∠3=∠ADE( )
∵∠3=∠B
∴∠B=∠ADE( )
∴ ∥BC( )
∴∠AED=∠C( )
18. 已知:如图,BD⊥AC于点D,EF⊥AC于点F,∠1+∠2=180°.求证:DGBC. 19. 按逻辑填写步骤和理由,将下面的证明过程补充完整.
19. 按逻辑填写步骤和理由,将下面的证明过程补充完整.如图, , 点A在直线a上,点B、C在直线b上,且 , 点D在线段上,连接AD,且平分 .

求证: .
证明:( )
( )
▲
(平角定义)
平分(已知)
▲ ( )
( )
(已知)
▲ ( )
(等量代换)
20. 按要求完成下列证明:如图,E点为DF上的点,B为AC上的点, , , 试说明: .
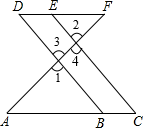
证明:
∵(已知),( ),
∴(等量代换).
∴▲( ).
∴( ).
又(已知),
∴(等量代换).
∴( ).
21. 如图,// , , EF平分 , , 垂足为点H,求的度数. 22. 如图①,已知AD∥BC,∠B=∠D=120°.
22. 如图①,已知AD∥BC,∠B=∠D=120°.
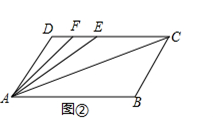 (1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.(3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出符合题意图形,并解答).23. 如图,BC//DE,CD、EF分别是∠ACB、∠AED的平分线.请完成以下过程.
(1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.(3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出符合题意图形,并解答).23. 如图,BC//DE,CD、EF分别是∠ACB、∠AED的平分线.请完成以下过程. (1)、请你猜想∠1与∠2的数量关系是 .(2)、完成以下推理过程:
(1)、请你猜想∠1与∠2的数量关系是 .(2)、完成以下推理过程:∵(已知),
∴∠ACB=∠ ▲ ( ).
又∵CD、EF分别是∠ACB、∠AED的平分线(已知),
∴ , ∠4= ▲ ( ).
∴∠3=∠4(等量代换),
∴// ▲ ( ).
∴∠1=∠2( ).
24. 如图所示,已知射线 , , 、在上,且满足 , 平分 , 根据上述条件,解答下列问题: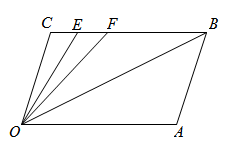 (1)、证明:;(2)、求的度数;(3)、若平行移动 , 那么的值是否随之变化?若不变,求出这个比值;若变化,请说明理由.25. 已知:如图,直线 , 点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.
(1)、证明:;(2)、求的度数;(3)、若平行移动 , 那么的值是否随之变化?若不变,求出这个比值;若变化,请说明理由.25. 已知:如图,直线 , 点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.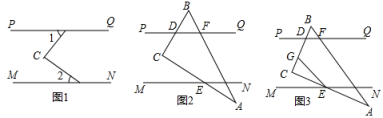 (1)、若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1∠2之间的数量关系.(2)、若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)、将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连结EG,且有∠CEG=∠CEM,给出下列两个结论:
(1)、若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1∠2之间的数量关系.(2)、若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)、将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连结EG,且有∠CEG=∠CEM,给出下列两个结论:①的值不变;
②∠GEN-∠BDF的值不变.
其中只有一个是正确的,你认为哪个是正确的?讲求出不变的值是多少.
26. 七年级同学解决平行线问题时,遇到这样的问题,请你帮忙解决:已知AB∥CD, (1)、如图1,猜想∠AEC,∠BAE,∠DCE之间有什么数量关系不必说明理由;(2)、如图2,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=40°,∠ABC=50°,求∠BED的度数;(3)、将图(2)中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请直接写出∠BED的度数(用含m,n的式子表示).
(1)、如图1,猜想∠AEC,∠BAE,∠DCE之间有什么数量关系不必说明理由;(2)、如图2,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=40°,∠ABC=50°,求∠BED的度数;(3)、将图(2)中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请直接写出∠BED的度数(用含m,n的式子表示).