2023年苏科版数学七年级下册全方位训练卷7.1探索直线平行的条件
试卷更新日期：2023-02-07 类型：同步测试
一、单选题（每题3分，共24分）
-
1. 如图，与∠1是同位角的是（ ）
A、∠2 B、∠3 C、∠4 D、∠52. 若直线 ， ， 相交如图所示，则的内错角为（ ）
A、 B、 C、 D、3. 如图，AB、CD被EF所截，则∠1与∠2是一对（ ）
A、同位角 B、内错角 C、同旁内角 D、都不是4. 如图，直线a，b被直线c所截，下列说法不正确的是（ ）
A、∠1与∠2是内错角 B、∠3与∠4是同旁内角 C、∠2与∠5是同位角 D、∠2与∠4是内错角5. 如图，∠1与∠2是（ ）
A、对顶角 B、同位角 C、内错角 D、同旁内角6. 如图，下列推论正确的是（ ）
A、 ， B、 ， C、 ， D、 ，7. 如图，点E在AB的延长线上，下列条件中能够判断AD∥BC的是（ ）
A、∠1＝∠3 B、∠C＝∠CBE C、∠C+∠ABC＝180° D、∠2＝∠48. 如图，点E在射线上，下列条件中能判断的是（ ）
A、 B、 C、 D、二、填空题（每题3分，共33分）
-
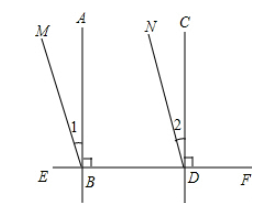
9. 如图，直线、被直线所截，交点分别为M、N，则的同位角是.
10. 用吸管吸易拉罐内的饮料时，如图所示，∠1＝108°，则∠2＝ ．
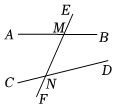
11. 如图，“4”字图中有a对同位角，b对内错角，c对同旁内角，则abc= ．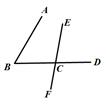
12. 如图，∠1与∠2是直线和被直线所截的一对角．
13. 如图，在△ABC和△ADE中，∠BAC =∠DAE=90°，∠B=50°，∠E=65°，则①∠1=∠3；②∠CAD+∠2=180°；③如果∠2=40°，则有BC∥AD；④如果∠2=30°，则有AC∥DE，上述结论中正确的是 .（填写序号）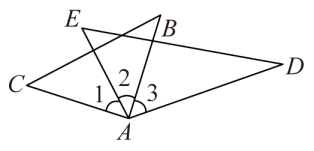
14. 如图所示，用直尺和三角尺作直线AB∥CD，这种作法的依据是.
15. 如图，四边形ABCD ， 点E是AB的延长线上的一点．请你添加一个条件，能判定 ． 这个条件是 ．
16. 如图，木工用角尺画出 ， 其依据是 ．
三、解答题（共10题，共93分）
-
17. 如图所示的图形中，同位角有多少对。
18. 如图，指出图中直线AC ， BC被直线AB所截的同位角、内错角、同旁内角．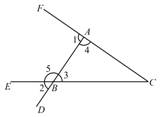
19.如图1，图2中，∠1和∠2，∠3和∠4各是哪两条直线被哪一条直线所截形成的？它们各是什么位置关系的角？
20. 看图填空：已知：如图，E为DF上的点，B为AC上的点，∠1 =∠2，∠C =∠D．求证：AC∥DF
证明：
∵∠1 =∠2（ ）
∠1 =∠3，∠2 =∠4（ ）
∴∠3 =∠4（ ）
∴ ▲ ∥ ▲ （ ）
∴∠C=∠ABD（ ）
又∵∠C =∠D（ ）
∴ ∠D=∠ABD（ ）
∴AC∥DF（ ）
21. 如图，在△ABC中，CD平分∠ACB，且∠ECD＝∠EDC．求证：DEAC．
22. 潜望镜是指从海面下伸出海面或从低洼坑道伸出地面，用以窥探海面或地面上活动的装置．其构造与普通地上望远镜相同，另加两个反射镜使从摄入潜望镜的光线经两次反射而折向眼中．潜望镜常用于潜水艇、坑道和坦克内用以观察敌情．如图，进入潜望镜的光线和离开潜望镜的光线是平行的，光线经过镜子反射时，∠1＝∠2，∠3＝∠4，请猜想潜望镜中两面镜子的位置关系，并说明理由．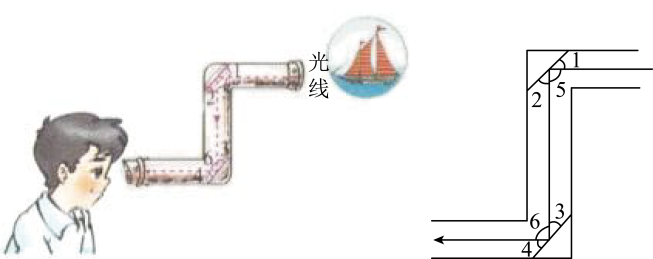
23. 如图所示，BF、DE相交于点A，BG交BF于点B，交AC于点C．
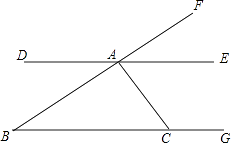(1)、指出ED、BC被BF所截的同位角，内错角，同旁内角；(2)、指出ED、BC被AC所截的内错角，同旁内角；(3)、指出FB、BC被AC所截的内错角，同旁内角．
