2023年苏科版数学八年级下册方位训练卷7.4频数分布表和频数分布直方图
试卷更新日期：2023-02-07 类型：同步测试
一、单选题（每题3分，共24分）
-
1. 一组数据的最大值是97，最小值是76，若组距是4，则可分为（ ）A、4组 B、5组 C、6组 D、7组2. 昆明某校七年级体育课上，体育老师统计了全班同学60秒跳绳的次数，发现跳绳次数最多的同学是185个，跳绳次数最少的同学是140个，为了分析数据需要列频数分布表，规定组距为6，那么组数是（ ）A、6 B、7 C、8 D、93. 将100个数据分成8个组，如下表所示，则第六组的频数为（ ）
租号
1
2
3
4
5
6
7
8
频数
11
14
12
13
13
x
12
10
A、12 B、13 C、14 D、154. 为了解某校初三年级学生的运算能力﹐抽取了100名学生进行测试，将所得成绩(单位：分)整理后，列出下表：分组
50~59
60~69
70~79
80～89
90~99
频数
6
16
8
30
40
本次测试的这100名学生的成绩为良好的(大于或等于80分为良好)频率是（ ）
A、0.22 B、0.30 C、0.60 D、0.705. 为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了仰卧起坐次数，并绘制如图所示的频数分布直方图，请根据图中的信息，计算仰卧起坐次数在∽次的百分比是（ ）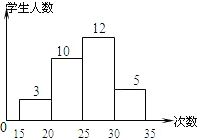
A、40% B、30% C、20% D、10%6. 某地在2022年4月空气质量等级统计图如下，则下列说法不正确的是（ ）
A、污染程度轻度及以上的天数占比20% B、空气质量优良等级的比例达到三分之二 C、污染程度轻微及以上的比例为三分之一 D、污染程度为中度的天数占比10%7. 小周是一位运动达人，他通过佩戴智能手环来记录自己一个月(30天)的每日行走步数(单位：千步)，并绘制成右面的统计图．根据统计图提供的信息，下列推断不合理的是（）
A、每日行走步数为4～8千步的天数占这个月总天数的10% B、每日行走步数为8～12千步的扇形圆心角是108° C、小周这个月超过一半的天数每日行走步数不低于12000步 D、小周这个月行走的总步数不超过324千步8. 对频数分布直方图的下列认识，错误的是（ ）A、每小组条形图的横宽等于这组的组距 B、每小组条形图的纵高等于这组的频数 C、每小组条形图的面积等于这组的频率 D、所有小组条形图的个数等于数据分组整理的组数二、填空题（每空3分，共30分）
-
9. 为了解八年级女生的体能情况，随机抽查了30名女生，测试了1分钟仰卧起坐的个数，并绘制成如图所示的频数分布直方图（每组含前一个边界，不含后个边界），则个数不低于38的有人．
10. 一组数据，其中最大值是170，最小值是147，对这组数据进行整理时，组距是4，则分成组合适．11. 为了了解本校七年级700名学生上学期参加社会实践活动的时间，随机对该年级50名学生进行了调查。根据收集的数据绘制了频数分布直方图，则下面四个说法中，符合题意说法的序号为 ． ①该频数分布直方图的组距是2；②可以推测七年级学生参加社会实践活动的时间在12~14h的人数最多；③被调查的学生参加社会实践活动时间不少于10h的占比为84%；④七年级学生中参加社会实践活动时间最多的是16h．
12. 为了了解学生参加家务劳动的情况，某中学随机抽取部分学生，统计他们双休日两天参加家务劳动的时间，将统计的劳动时间x（单位：min）分成5组： ， ， ， ， ， 绘制成如图所示的频数分布直方图．根据图中提供的信息，可知这次抽样调查的样本频数最大的一组的组中值为min．
13. 某校200名学生参加生命安全知识测试，测试分数均大于或等于60且小于100，分数段的频率分布情况如表所示，结合表的信息，可得测试分数在79.5～89.5分数段的学生有名.分数段
59.5～69.5
69.5～79.5
79.5～89.5
89.5～99.5
频率
0.1
0.3
0.2
14. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表，则表中a= ， b= ， c= ．月均用水量/t
频数
2
12
a
10
b
3
2
百分比
4％
24％
c
20％
12％
6％
4％
15. 为了考察某种大麦穗长的分布情况，在一块试验田抽取了100个麦穗，量出它们的长度．在样本数据中，最大值是 ， 最小值是 ． 列频数分布表时，若取组距为0.3，则适合的组数是 ．16. 为了解新冠肺炎疫情解封后刚复学时学生的心理健康，扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查，对500个数据进行整理，在频数的统计表中各组的频数之和等于 ．三、解答题（共10题，共96分）
-
17. 在某段公路上，最高限速65km/h.交警部门设置了雷达探测器监测汽车的行驶速度，以下是交警部门某天一段时间内记录的驶过该处的30辆车的行驶速度（单位：km/h）；
55 49 61 47 49 54 49 57 59 58
50 51 48 49 80 58 48 54 70 71
62 45 56 64 78 52 60 55 49 75
请按组距为10进行分组，列出频数分布表，画出频数分布直方图，并分析有几辆车超速.
18. 为了了解中学生的身体发育情况，对某中学同年龄的60名女学生的身高进行了测量．结果如下．（单位：厘米）（投影片）158 167 154 159 166 169 159156 166 162 159 156 166 164 160 157 156 160 157 161 158158 153 158 164 158 163 158 153 157 162 162 159 154 165166 157 151 146 151 158 160 165 158 163 162 161 154 163165 162 162 159 157 159 149 164 168 159 153
我们知道，这组数据的平均数，反映了这些学生的平均身高．但是，有时只知道这一点还不够，还希望知道身高在哪个范围内的学生多，在哪个小范围内的学生少，也就是说，希望知道这60名女学生的身高数据在各个小范围内所占的比的大小．
19. 为了了解中学生的身体发育情况，对某中学同龄的50名男生的身高进行了测量，结果如下（单位：cm）：162、166、163、174、175、172、177、161、171、172、172、175、169、157、173、173、166、174、166、169、160、158、159、166、167、182、166、175、167、174
、179、173、180、172、 173、174、165、172、163、165、170、175、170、171、176、169
、171、167、165、177
如果按照3cm的组距分组，可以分成9组：156.5～159.5、159.5～162.5、162.5～165.5、165.5
～168.5、168.5～171.5、171.5～174.5、174.5～177.5、177.5～180.5、180.5～183.5
(1)、落在哪个小组的人数最多？是多少？(2)、落在哪个小组的人数最少？是多少？20. 某学校20名数学教师的年龄（单位：岁）情况如下：29，42，58，37，53，52，49，24，37，46，42，55，40，38，50，26，54，26，44，52．(1)、填写下面的频率分布表：分组
频数
频率
19.5～29.5
29.5～39.5
39.5～49.5
49.5～59.5
合计
(2)、画出数据的频数分布直方图．21. 某县八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的得分进行统计．请你根据不完整的表格，解答下列问题：（1）补全频数分布表；
（2）随机抽取的样本容量为多少；
（3）若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．估计这3000名学生中，有多少学生得分等级为A？
成绩 x 分
频 数
频 率
50≤x＜60
10
60≤x＜70
16
0.08
70≤x＜80
0.2
80≤x＜90
62
0.31
90≤x＜100
72
0.36
22. 某校七年级开展了“勿忘历史，吾辈自强”历史知识竞赛活动，并随机抽取部分学生成绩作为样本进行分析，绘制成如下的统计表（每组成绩含前一个分数，不含后一个分数，最后一组前后分数均包含）：
成绩/分
频数
百分比
第1段
50～60
2
4%
第2段
60～70
6
12%
第3段
70～80
9
b
第4段
80～90
a
36%
第5段
90～100
15
30%
请根据所给信息，解答下列问题
(1)、a= ， b=；(2)、请补全频数分布直方图：(3)、现要将调查结果绘制成扇形统计图，求成绩在“90～100”这一分数段所对应的扇形圆心角是多少度？23. 为了解青少年身体发育情况，学校每年定期为学生进行生长情况监测．七年一班18名女生身高情况如下（单位：）：155 162 150 154 157 149 151 168 156 147 152 162 166 159 153 158 164 160下面是频数分布直方图的一部分，请回答问题：
(1)、最大值与最小值的差是；(2)、如果取组距为5，那么可以分为组；(3)、请补全直方图；(4)、学校将要召开运动会，身高不低于 ， 不高于学生可以入选花束队，七年一班可以有多少名女生符合资格要求？24. 为落实“双减”政策（“双减”指有效减轻义务教育阶段学生过重作业负担和校外培训负担），某校积极开展“双诚”政策的宣传活动．为了解学生对“双减”政策的态度，该校随机抽取了部分学生进行调查，并绘制了如下的统计图表（部分信息未给出）．态度
频数（人数）
频率
非常喜欢
5
0.05
喜欢
0.35
一般
50
n
不喜欢
10
合计
m
1
(1)、在上面的统计表中m= ， n= ．(2)、请将条形统计图补充完整．(3)、请结合以上统计信息，谈一下你的体会．25. 为了解某校七年级学生身高情况，随机测量了m位同学的身高（单位：cm），并根据测得的数据绘制了两幅不完整的统计图（A.150~155，B.155~160，C.160~165，D.165~170，E.170~175），请结合图中提供的信息，解答下列问题：
(1)、m= ， C所在扇形的圆心角度数是°；(2)、补全频数分布直方图；(3)、若该校七年级计划开展大课间体操比赛，要求每班应安排不低于本班人数30%的学生参加，并希望参赛学生的身高差距较小，请问你觉得应安排哪个范围的学生参赛更合适，并说说你的理由．26. 为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下成绩得分均为整数：组别
成绩分组
频数
百分比
1
2
5%
2
4
10%
3
20%
4
10
25%
5
6
15%
合计
40
100%
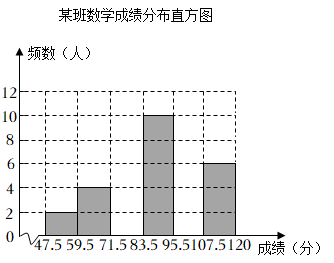
根据表中提供的信息解答下列问题：
(1)、频数分布表中的 ， ， ；(2)、已知全区八年级共有200个班平均每班40人 ， 用这份试卷检测，108分及以上为优秀，预计优秀的人数约为人，72分及以上为及格，预计及格的人数约为人，及格的百分比约为；(3)、补充完整频数分布直方图．