贵州省毕节市2021-2022学年七年级下学期阶段性练习数学试题
试卷更新日期:2023-02-07 类型:月考试卷
一、单选题
-
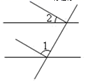
1. 下列运算正确的是( )A、 B、 C、 D、2. 下面四个图形中, 与 是同位角的是( )A、
 B、
B、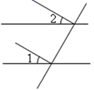 C、
C、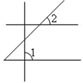 D、
D、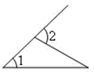 3. 氧原子直径大约是0.0000000016m,将0.0000000016用科学记数法表示是( )A、 B、 C、 D、4. 计算的结果是( )A、 B、 C、 D、5. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
3. 氧原子直径大约是0.0000000016m,将0.0000000016用科学记数法表示是( )A、 B、 C、 D、4. 计算的结果是( )A、 B、 C、 D、5. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、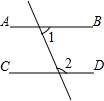 B、
B、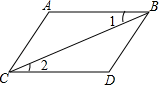 C、
C、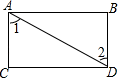 D、
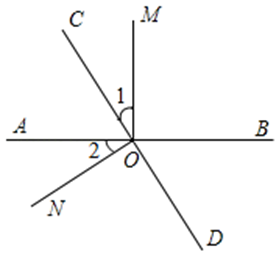
D、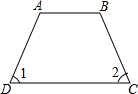 6. 已知 , , 则的值是( )A、2 B、1 C、4 D、57. 如果是完全平方式,则( )A、16 B、4 C、4或-4 D、2或-28. 如图,.如果 , 那么的度数是( )
6. 已知 , , 则的值是( )A、2 B、1 C、4 D、57. 如果是完全平方式,则( )A、16 B、4 C、4或-4 D、2或-28. 如图,.如果 , 那么的度数是( )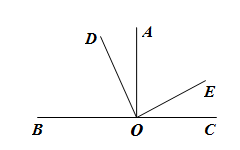 A、90° B、118° C、122° D、1559. 下列各式中能用平方差公式计算的是( )A、 B、 C、 D、10. 计算:( )A、1 B、-1 C、2 D、-211. , 则p的值是( )A、-3 B、8 C、-8 D、-512. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )
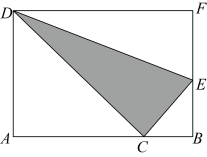
A、90° B、118° C、122° D、1559. 下列各式中能用平方差公式计算的是( )A、 B、 C、 D、10. 计算:( )A、1 B、-1 C、2 D、-211. , 则p的值是( )A、-3 B、8 C、-8 D、-512. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )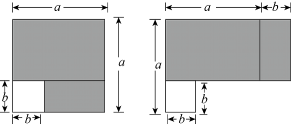 A、 B、 C、 D、13. 已知M= , 则M=( )A、 B、 C、 D、14. 已知 , 那么的值是( )A、2022 B、1 C、 D、15. 如图,两个正方形的边长分别为a,b(a>b),如果a+b=10,ab=16,则阴影部分的面积是( )
A、 B、 C、 D、13. 已知M= , 则M=( )A、 B、 C、 D、14. 已知 , 那么的值是( )A、2022 B、1 C、 D、15. 如图,两个正方形的边长分别为a,b(a>b),如果a+b=10,ab=16,则阴影部分的面积是( )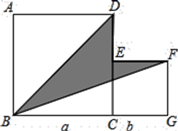 A、16 B、13 C、26 D、30
A、16 B、13 C、26 D、30二、填空题
-
16. 已知一个角的度数为 , 则它的余角度数等于.17. 若 , , 则.18. 如图,若要使与平行,则绕点O旋转的度数至少是.
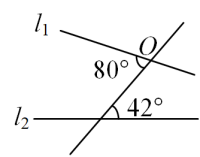 19. 若与的乘积中不含x的一次项,则实数a的值为.20. 若m(m-2)=1,则(m-1)2的值是 .
19. 若与的乘积中不含x的一次项,则实数a的值为.20. 若m(m-2)=1,则(m-1)2的值是 .三、解答题
-
21. 计算:(1)、;(2)、.22. 先化简,再求值: , 其中.23. 如图,直线、、相交于点O,且 , 平分 , 若 , 求的度数.
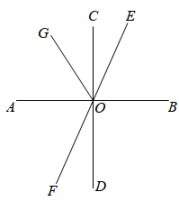 24. 按要求解答下列各小题(1)、已知 , , 求的值;(2)、如果 , 求的值;(3)、已知 , 求m的值.25. 图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
24. 按要求解答下列各小题(1)、已知 , , 求的值;(2)、如果 , 求的值;(3)、已知 , 求m的值.25. 图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.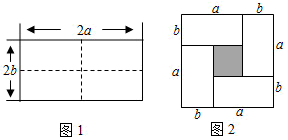 (1)、图2中阴影部分的正方形边长为.(2)、请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.(3)、已知 , , 求
(1)、图2中阴影部分的正方形边长为.(2)、请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.(3)、已知 , , 求