贵州省安顺市开发区2021-2022学年九年级下学期5月月考数学试题

试卷更新日期：2023-02-07 类型：月考试卷

进入出卷网下载

一、单选题

1. 在实数0， $π$ ， $| - 3 |$ ， $- 2$ 中，最小的数是（）

A、0 B、 $π$ C、 $| - 3 |$ D、 $- 2$

查看试题解析
2. 下列几何体中，其俯视图与主视图相同的是（）

A、 B、 C、 D、

查看试题解析
3. 贵州黔北（德江）民用机场项目建设于2021年12月15日正式启动，该工程总投资约21.5亿元.将21.5亿用科学记数法表示为（）

A、 $0.215 \times 1 0^{10}$ B、 $21.5 \times 1 0^{8}$ C、 $2.15 \times 1 0^{9}$ D、 $2.15 \times 1 0^{10}$

查看试题解析
4. 下列运算正确的是（）

A、 $2 a^{2} + a^{3} = 2 a^{5}$ B、 ${(- 2 a^{2})}^{3} = - 8 a^{8}$ C、 $(- a^{6}) \div (- a)^{2} = - a^{4}$ D、 $(a - 1)^{2} = a^{2} - 1$

查看试题解析
5. 某小组同学在一周内参加家务劳动的时间统计如下表，下列说法正确的是（）
劳动时间/h
3
3.5
4
4.5
人数
1
1
2
1

A、中位数是3.75，众数是4 B、中位数是3.5，众数是4 C、中位数是4，众数是4 D、中位数是4，众数是2

查看试题解析
6. 已知点 $M (a ， 2)$ 在第二象限，且 $| a | = 1$ ，则点M关于原点对称的点的坐标是（）

A、 $(- 2 ， 1)$ B、 $(- 1 ， 2)$ C、 $(2 ， - 1)$ D、 $(1 ， - 2)$

查看试题解析
7. 如图的电路图上有4个开关 $A ， B ， C ， D$ 和1个小灯泡下列操作中，“小灯泡发光”这个事件是随机事件的是（）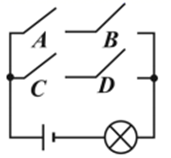

A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关

查看试题解析
8. 在△ABC中，∠ACB＝90°，AC＝BC，AB＝10，用尺规作图的方法作线段AD和线段DE，保留作图痕迹如图所示，认真观察作图痕迹，则△BDE的周长是（）

A、8 B、5 $\sqrt{2}$ C、 $\frac{15 \sqrt{2}}{2}$ D、10

查看试题解析
9. 若关于x的一元一次方程 $\frac{1}{2022} x + 3 = 2 x + b$ 的解为 $x = - 3$ ，则关于y的一元一次方程 $\frac{1}{2022} (y + 1) + 3 = 2 (y + 1) + b$ 的解为（）

A、 $y = 1$ B、 $y = - 2$ C、 $y = - 3$ D、 $y = - 4$

查看试题解析
10. 某小区内的消防车道有一段弯道，如图，弯道的内外边缘均为圆弧， $\overset{⌢}{A B}$ ， $\overset{⌢}{C D}$ 所在圆的圆心为O，点C，D分别在OA，OB上，已知消防车道半径OC=12m，消防车道宽AC=4m， $∠ A O B = 120 °$ ，则弯道外边缘 $\overset{⌢}{A B}$ 的长为（）

A、 $8 π m$ B、 $4 π m$ C、 $\frac{32}{3} π m$ D、 $\frac{16}{3} π m$

查看试题解析
11. 如图，过 $x$ 轴正半轴上的任意点 $P$ ，作 $y$ 轴的平行线，分别与反比例函数 $y = \frac{2}{x} (x > 0)$ 和 $y = - \frac{4}{x} (x > 0)$ 的图象交于 $B$ 、 $A$ 两点．若点 $C$ 是 $y$ 轴上任意一点，则 $△ A B C$ 的面积为（）

A、4 B、3 C、2 D、1

查看试题解析
12. 已知二次函数 $y = (x - a - 1) (x - a + 1) - 2 a + 9$ （a是常数）的图象与x轴没有公共点，且当 $x < - 2$ 时，y随x的增大而减小，则实数a的取值范围是（）

A、 $a < 4$ B、 $- 2 < a < 4$ C、 $- 2 \leq a < 4$ D、 $- 2 < a \leq 4$

查看试题解析

二、填空题

13. 若 $\frac{1}{\sqrt{3 - x}}$ 在实数范围内有意义，则实数x的取值范围是 .

查看试题解析
14. 如图，在平面直角坐标系中， $▱ A B C D$ 的顶点A，B在x轴上，顶点D在y轴的正半轴上.若 $A D = 5 ， A B = 9 ， A (- 3 ， 0)$ ，则点C的坐标为.

查看试题解析
15. 如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA＝度.

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A D = 8$ ， $A B = 6$ ，将矩形 $A B C D$ 绕点 $D$ 顺时针旋转得到矩形 $E F G D$ ，边 $B C$ 与 $D E$ 交于点 $P$ ，延长 $B C$ 交 $F G$ 于点 $Q$ ，若 $B Q = 2 B P$ ，则 $B P$ 的长为.

查看试题解析

三、解答题

17. 在如图1、图2的 $6 \times 5$ 网格中，每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上.

(1)、在图1中画一个以线段 $A B$ 为腰的等腰三角形，所画等腰三角形各顶点必须在小正方形的顶点上，且底边长是有理数；

(2)、在图2中画一个以线段 $A B$ 为边的菱形（非正方形），所画菱形各顶点必须在小正方形的顶点上.

查看试题解析
18. 为了弘扬美食文化，助力黔菜出山，某数学兴趣小组在国际广场展开了“舌尖上的贵阳一我最喜爱的贵阳小吃”的随机调查，并给出四种选择（A.丝娃娃，B.肠旺面，C.老素粉，D.豆腐果），每人选且只选一种，该兴趣小组将调查得到的数据整理后，绘制成如下两幅不完整的统计图.
根据以上信息，解答下列问题：

(1)、本次共调查了 ▲ 人，请补全条形统计图；

(2)、已知西秀区人口约87万人，估计西秀区市民中最喜欢老素粉的有万人；

(3)、“五·一”小长假期间，小度打算去贵阳旅游，并从以上四种小吃中随机选择两种不同的小吃进行品尝，请用列表或画树状图的方法求小度选中肠旺面和豆腐果的概率.

查看试题解析
19. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，过点D作 $D E ∥ B C$ 交 $A B$ 于点E， $D F ∥ A B$ 交 $B C$ 于点F.

(1)、判断四边形 $B E D F$ 的形状，并说明理由；

(2)、若 $∠ A B C = 60 °$ ， $∠ A C B = 45 °$ ， $C D = 6$ ，求 $D F$ 的长.

查看试题解析
20. 如图，一次函数 $y = m x + n$ 的图象与反比例函数 $y = \frac{k}{x}$ 点的图象交于点 $A (- 2 ， a)$ ， $B (1 ， - 2)$ .

(1)、求一次函数和反比例函数的解析式；

(2)、若直线 $A B$ 上有一点P，且 $P O = P A$ ，求点P的坐标.

查看试题解析
21. 图①是一辆登高云梯消防车的实物图，图②是其工作示意图，起重臂 $A C$ 是可伸缩的（ $10 m ⩽ A C ⩽ 20 m$ ），且起重臂 $A C$ 可绕点A在一定范围内转动，张角为 $∠ C A E (90 ° ⩽ ∠ C A E ⩽ 150 °)$ ，转动点A距离地面 $B D$ 的高度 $A E$ 为 $3.5 m$ ．

(1)、当起重臂 $A C$ 长度为 $12 m$ ，张角 $∠ C A E$ 为 $120 °$ 时，求云梯消防车最高点C距离地面的高度 $C F$ ；

(2)、某日、一居民家突发险情，该居民家距离地面的高度为 $18 m$ ，请问该消防车能否实施有效救援？（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
22. 为响应传统文化进校园的号召，某校决定从网店购买《论语》和《弟子规》两种图书以供学生课外阅读.已知两种图书的购买信息如下表：
《论语》数量/本
《弟子规》数量/本
总费用（元）
40
30
1250
50
20
1300

(1)、《论语》和《弟子规》每本的价格分别是多少元？

(2)、若学校计划购买《论语》和《弟子规》两种图书共100本，《弟子规》的数量不超过《论语》数量的2倍.请设计出最省钱的购买方案，并求出此方案的总费用.

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，以AB为直径的 $⊙ O$ 交BC于点D，过点D作 $D E ⊥ A C$ ，交AC于点E，AC的反向延长线交 $⊙ O$ 于点F.

(1)、求证：DE为 $⊙ O$ 的切线；

(2)、若 $D E + E A = 8$ ， $⊙ O$ 的半径为10，求 $A F$ 的长度.

查看试题解析
24. 如图是小明站在点O处长抛篮球的路线示意图，球在点A处离手，且 $O A = 1 m$ .第一次在点D处落地，然后弹起在点E处落地，篮球在距O点 $6 m$ 的点B处正上方达到最高点，最高点C距地面的高度 $B C = 4 m$ ，点E到篮球框正下方的距离 $E F = 2 m$ ，篮球框的垂直高度为 $3 m$ .据试验，两次划出的抛物线形状相同，但第二次的最大高度为第一次的 $\frac{1}{2}$ ，以小明站立处点O为原点，建立如图所示的平面直角坐标系.

(1)、求抛物线 $A C D$ 的函数解析式；

(2)、求篮球第二次的落地点E到点O的距离.（结果保留整数）

(3)、若小明想一次投中篮球框，他应该向前走多少米？（结果精确到 $0.1 m$ ）（参考数据： $\sqrt{3} \approx 1.73 ， \sqrt{6} \approx 2.45$ ）

查看试题解析
25. 【问题情境】如图1，在等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， F是 $A C$ 边上一动点（点F不与点A，C重合），以 $C F$ 为边在 $△ A B C$ 外作正方形 $C D E F$ ，连接 $A D$ ， $B F$ .

(1)、【探究展示】①猜想：图1中，线段 $B F$ ， $A D$ 的数量关系是，位置关系是 .
②如图2，将图1中的正方形 $C D E F$ 绕点C顺时针旋转 $α$ ， $B F$ 交 $A C$ 于点H，交 $A D$ 于点O，①中的结论是否仍然成立？请说明理由.

(2)、【拓展延伸】如图3，将【问题情境】中的等腰直角三角形 $A B C$ 改为直角三角形 $A B C$ ， $∠ A C B = 90 °$ ，正方形 $C D E F$ 改为矩形 $C D E F$ ，连接 $B F$ 并延长，交 $A C$ 于点H，交 $A D$ 于点O，连接 $B D$ ， $A F$ .若 $A C = 4$ ， $B C = 3$ ， $C D = \frac{4}{3}$ ， $C F = 1$ ，求 $B D^{2} + A F^{2}$ 的值.

查看试题解析

《论语》数量/本	《弟子规》数量/本	总费用（元）
40	30	1250
50	20	1300

劳动时间/h	3	3.5	4	4.5
人数	1	1	2	1