贵州省安顺市2021-2022学年九年级下学期4月月考数学试题
试卷更新日期:2023-02-07 类型:月考试卷
一、单选题
-
1. 下列实数中是无理数的是( )A、 B、27 C、 D、2. 如图所示的几何体的左视图是( )
 A、
A、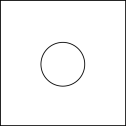 B、
B、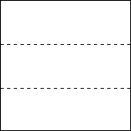 C、
C、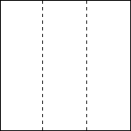 D、
D、 3. 清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、4. 如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是( )
3. 清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、4. 如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是( )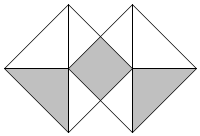 A、 B、 C、 D、5. 用尺规作图法作已知角的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧在的内部相交于点C;③作射线OC. 则射线OC为的平分线,由上述作法可得的依据是( )
A、 B、 C、 D、5. 用尺规作图法作已知角的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧在的内部相交于点C;③作射线OC. 则射线OC为的平分线,由上述作法可得的依据是( )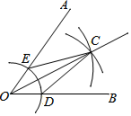 A、SAS B、AAS C、ASA D、SSS6. 原价为元的某商品经过两次降价后,现售价元,如果每次降价的百分比都为 , 则下列各式正确的是( )A、 B、 C、 D、7. 已知正比例函数的图象经过第二、四象限,则一次函数的图象可能是( )A、
A、SAS B、AAS C、ASA D、SSS6. 原价为元的某商品经过两次降价后,现售价元,如果每次降价的百分比都为 , 则下列各式正确的是( )A、 B、 C、 D、7. 已知正比例函数的图象经过第二、四象限,则一次函数的图象可能是( )A、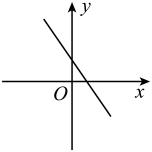 B、
B、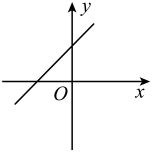 C、
C、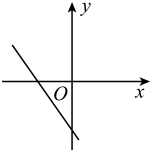 D、
D、 8. 如图,AB是 的直径,弦 于点E, ,则 的度数为( )
8. 如图,AB是 的直径,弦 于点E, ,则 的度数为( )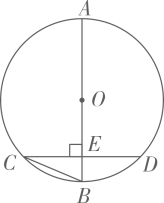 A、 B、 C、 D、9. 已知 , , ,则 的值为( )A、16 B、12 C、10 D、无法确定10. 如图,在Rt△ABC中, , BC=2AC,以AC,BC为边向外作正方形ACDE和正方形BCFG,N为BC上一点,连接FN并延长,交EA的延长线于点M,则的值是( )
A、 B、 C、 D、9. 已知 , , ,则 的值为( )A、16 B、12 C、10 D、无法确定10. 如图,在Rt△ABC中, , BC=2AC,以AC,BC为边向外作正方形ACDE和正方形BCFG,N为BC上一点,连接FN并延长,交EA的延长线于点M,则的值是( )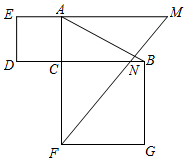 A、 B、 C、 D、11. 如图,顶点为的抛物线经过点 , 则下列结论中正确的是( )
A、 B、 C、 D、11. 如图,顶点为的抛物线经过点 , 则下列结论中正确的是( )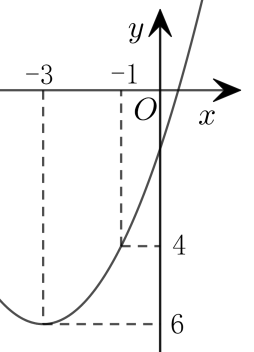 A、 B、若点都在抛物线上,则 C、当时,y随x的增大而减小 D、关于x的一元二次方程有两个不等的实数根12. 如图,点A是双曲线y=是第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A、 B、若点都在抛物线上,则 C、当时,y随x的增大而减小 D、关于x的一元二次方程有两个不等的实数根12. 如图,点A是双曲线y=是第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )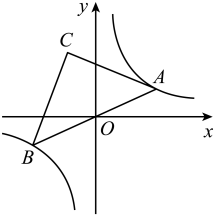 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 甲、乙、丙三人进行射击测试,已知三人近10次射击成绩的平均数都是7.8环,方差分别是 , 则射击成绩最稳定的是.14. 如图, ,垂足为 , ,则 的度数为.
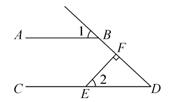 15. 若关于x的方程的解是非负数,则m的取值范围是.16. 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一条直线上,连结BD、BE,下面四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AB2+AD2),其中正确的结论是 (只需填写序号).
15. 若关于x的方程的解是非负数,则m的取值范围是.16. 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一条直线上,连结BD、BE,下面四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AB2+AD2),其中正确的结论是 (只需填写序号).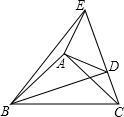
三、解答题
-
17.(1)、计算:;(2)、解一元二次方程:.18. 某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调查,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
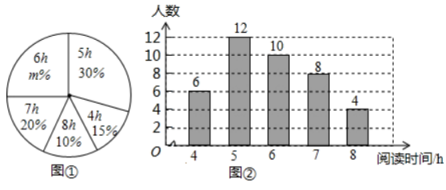
(Ⅰ)本次接受随机抽样调查的学生人数为 , 图①中的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于的学生人数.
19. 如图,菱形的对角线 , 相交于点O,E是的中点,点F,G在边上,且 , .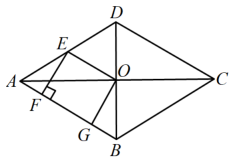 (1)、判断四边形的形状,并说明理由;(2)、若 , , 求和的长.20. 某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车,2名熟练工和3名新工人每月可安装14辆电动汽车(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?21. 资阳市为实现5G网络全覆盖,2020-2025年拟建设5G基站七千个.如图,在坡度为的斜坡上有一建成的基站塔 , 小芮在坡脚C测得塔顶A的仰角为 , 然后她沿坡面行走13米到达D处,在D处测得塔顶A的仰角为(点A、B、C、D均在同一平面内)(参考数据:)
(1)、判断四边形的形状,并说明理由;(2)、若 , , 求和的长.20. 某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车,2名熟练工和3名新工人每月可安装14辆电动汽车(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?21. 资阳市为实现5G网络全覆盖,2020-2025年拟建设5G基站七千个.如图,在坡度为的斜坡上有一建成的基站塔 , 小芮在坡脚C测得塔顶A的仰角为 , 然后她沿坡面行走13米到达D处,在D处测得塔顶A的仰角为(点A、B、C、D均在同一平面内)(参考数据:)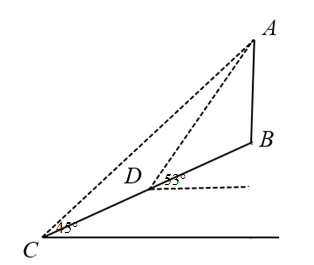 (1)、求D处的竖直高度;(2)、求基站塔的高.22. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于两点,与y轴交于点C.
(1)、求D处的竖直高度;(2)、求基站塔的高.22. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于两点,与y轴交于点C.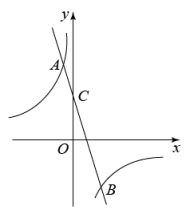 (1)、求一次函数的解析式;(2)、根据图象,直接写出关于x的不等式的解集;(3)、若P是x轴上一点,且的面积是面积的3倍,求点P的坐标.23. 如图,抛物线.与x轴交于A,B两点,与y轴交于直线经过点A且与抛物线交于另一点D.
(1)、求一次函数的解析式;(2)、根据图象,直接写出关于x的不等式的解集;(3)、若P是x轴上一点,且的面积是面积的3倍,求点P的坐标.23. 如图,抛物线.与x轴交于A,B两点,与y轴交于直线经过点A且与抛物线交于另一点D. (1)、求抛物线的解析式;(2)、若P是位于直线上方的抛物线上的一个动点,连接 , 求的面积的最大值.24. 如图,已知:AB为⊙O的直径,⊙O交△ABC于点D、E,点F为AC的延长线上一点,且∠CBF ∠BOE.
(1)、求抛物线的解析式;(2)、若P是位于直线上方的抛物线上的一个动点,连接 , 求的面积的最大值.24. 如图,已知:AB为⊙O的直径,⊙O交△ABC于点D、E,点F为AC的延长线上一点,且∠CBF ∠BOE.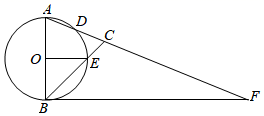 (1)、求证:BF是⊙O的切线;(2)、若AB=4 ,∠CBF=45°,BE=2EC,求AD和CF的长.25. 【问题探究】
(1)、求证:BF是⊙O的切线;(2)、若AB=4 ,∠CBF=45°,BE=2EC,求AD和CF的长.25. 【问题探究】数学实践小组的同学利用一张宽的矩形纸片进行了如下的操作写探究:
第一步:如图1,将该矩形纸片沿过点D的直线折叠,使点A落在上的点处,得到折痕 , 然后把纸片展平.
第二步:如图2,将图1中的矩形纸片沿过点E的直线折叠,使点C恰好落在上的点处,点B落在点处,得到折痕 , 交于点M,交于点N,再把纸片展平.
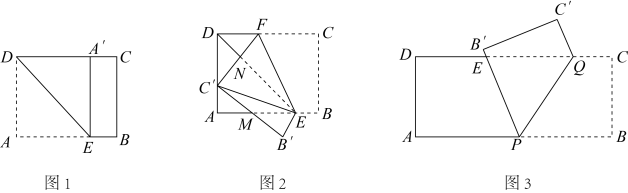 (1)、【问题解决】
(1)、【问题解决】如图1,填空:四边形的形状是.
(2)、如图2,小明连接了 , E两点,发现线段写是相等的.①请帮助小明写出证明过程;
②如图2,若 , 求的值.
(3)、【问题延伸】如图3,若该矩形纸片的长 , 点Q在边上,且 , P是边上的动点(不与点A,B重合).现将纸片沿折叠,使点B,C分别落在点 , 处.在点P从点A向点B运动的过程中,若边与边交于点E,则点E相应运动的路径长为.