湖南省益阳市2022-2023学年高三上学期数学期末试卷
试卷更新日期:2023-02-06 类型:期末考试
一、单选题
-
1. 已知全集 , 集合 , 则为( )A、 B、 C、 D、2. 设复数 , 则( )A、 B、 C、 D、3. 如图所示的矩形中,满足 , 为的中点,若 , 则的值为( )
 A、 B、 C、 D、24. 在一次劳动技术课上,某12人的小组中的同学们利用图(一)的棱长为的正方体胶泥作为原料,每人制作一个图(二)的冰激淋胶泥模型(上部分为一个半球,下部分为一个以半球的大圆面为底的圆锥),则制作完成后剩下的胶泥约为( )(忽略制作过程中的损耗,)
A、 B、 C、 D、24. 在一次劳动技术课上,某12人的小组中的同学们利用图(一)的棱长为的正方体胶泥作为原料,每人制作一个图(二)的冰激淋胶泥模型(上部分为一个半球,下部分为一个以半球的大圆面为底的圆锥),则制作完成后剩下的胶泥约为( )(忽略制作过程中的损耗,) A、 B、 C、 D、5. 已知函数 , 若 , 则的值为( )A、 B、 C、 D、6. 年10月12日“天宫课堂”首次在问天实验舱中授课,航天员老师们演示和讲解的多种实验,极大地激发了学生的学习兴趣.在一次模仿操作实验中,学生们从装有大小相同的标号分别为的9种不同的种子中随机抽取2种种子进行操作实验,则抽到的两种不同的种子的标号之和恰为10的概率为( )A、 B、 C、 D、7. 已知函数 , 若 , , 则对应的值为( )A、 B、 C、 D、8. 已知函数 , 若方程有3个不等的实根,则实数的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、5. 已知函数 , 若 , 则的值为( )A、 B、 C、 D、6. 年10月12日“天宫课堂”首次在问天实验舱中授课,航天员老师们演示和讲解的多种实验,极大地激发了学生的学习兴趣.在一次模仿操作实验中,学生们从装有大小相同的标号分别为的9种不同的种子中随机抽取2种种子进行操作实验,则抽到的两种不同的种子的标号之和恰为10的概率为( )A、 B、 C、 D、7. 已知函数 , 若 , , 则对应的值为( )A、 B、 C、 D、8. 已知函数 , 若方程有3个不等的实根,则实数的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 如图为国家统计局于2022年11月15日发布的社会消费品零售总额同比增速折线图,则2021年10月至2022年10月同比增速的( )(注:2022年月份合并统计为一个数据)
 A、平均数大于0 B、中位数为 2.7 C、极差为17.8 D、第 25 百分位数为10. 已知函数 , 则( )A、有2个极大值点 B、有1个极小值点 C、 D、点处的切线方程为11. 已知双曲线 , 则( )A、C的离心率为 B、的渐近线方程为 C、直线与有2个公共点 D、过右焦点的直线与的交点分别为 , 当时,这样的直线有3条12. 已知函数及其导函数的定义域均为 , 记 , 若关于直线对称,为奇函数,则( )A、 B、 C、 D、
A、平均数大于0 B、中位数为 2.7 C、极差为17.8 D、第 25 百分位数为10. 已知函数 , 则( )A、有2个极大值点 B、有1个极小值点 C、 D、点处的切线方程为11. 已知双曲线 , 则( )A、C的离心率为 B、的渐近线方程为 C、直线与有2个公共点 D、过右焦点的直线与的交点分别为 , 当时,这样的直线有3条12. 已知函数及其导函数的定义域均为 , 记 , 若关于直线对称,为奇函数,则( )A、 B、 C、 D、三、填空题
-
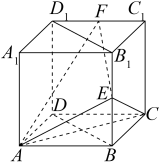
13. 的展开式中含项的系数为(用数字作答).14. 已知长方体中, , 点为棱的中点,则异面直线所成角的余弦值为.15. 已知圆 , 圆的圆心在轴上,过点 , 若圆与圆外切,则圆的方程为.16. 已知抛物线的焦点为 , 圆与交于两点,其中点在第一象限,点在直线上运动,记.
①当时,有;
②当时,有;
③可能是等腰直角三角形;
其中命题中正确的有.
四、解答题
-
17. 已知数列的前项和为 , 且.(1)、求的通项公式;(2)、若 , 求.18. 在中,角的对边分别为 , 且.(1)、求;(2)、证明:.19. 某学校为推动学校的大课间运动,开始在部分班级中使用一套新的大课间运动体操(记为A类体操),原来的大课间运动体操(记为B类体操),为了解学生对大课间运动的喜爱程度与使用大课间运动体操类别是否有关,分别对使用A类体操与B类体操的学生进行了问卷调查,现分别随机抽取了100个学生的问卷调查情况,得到如下数据:
喜爱
不喜爱
A类体操
70
30
B类体操
40
60
附: ,
(1)、试根据小概率值的独立性检验,能否认为喜爱大课间运动程度与A类体操和B类体操有关?(2)、从样本的喜爱大课间运动的学生中,按A、B类分层抽取11名学生参加一个座谈会,再从中抽取3名学生在学生大课间运动会上发言,求参加发言的学生既有喜爱A类体操也有喜爱B类体操的概率.