湖北省新高考联考协作体2022-2023学年高三上学期期末联考数学试题
试卷更新日期:2023-02-06 类型:期末考试
一、单选题
-
1. 已知集合 , 则A的子集共有( )个A、3 B、4 C、6 D、72. 若复数z满足(其中i是虚数单位),复数z的共轭复数为 , 则( )A、z的实部是 B、z的虚部是 C、复数在复平面内对应的点在第一象限 D、3. 2022年9月16日,接迎第九批在韩志愿军烈士遗骸回国的运20专机在两架歼20战机护航下抵达沈阳国际机场,歼20战机是我国自主研发的第五代最先进的战斗机,它具有高隐身性、高态势感知、高机动性能等特点,歼20机身头部是一个圆锥形,这种圆锥的轴截面是一个边长约为2米的正三角形,则机身头部侧面积约为( )平方米A、 B、 C、 D、4. “”是“方程表示焦点在y轴上的椭圆”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知是各项均为正数的等差数列,为其前n项和,且 , 则当取最大值时,( )A、10 B、20 C、25 D、506. 已知 , 则( )A、 B、 C、 D、7. 已知函数 , 且(其中e为自然对数的底数,为圆周率),则a,b,c的大小关系为( )A、 B、 C、 D、8. 2022卡塔尔世界杯比赛场地是在卡塔尔的8座体育馆举办.将甲、乙、丙、丁4名裁判随机派往卢赛尔,贾努布,阿图玛玛三座体育馆进行执法,每座体育馆至少派1名裁判,A表示事件“裁判甲派往卢赛尔体有馆”;B表示事件“裁判乙派往卢赛尔体育馆”;C表示事件“裁判乙派往贾努布体育馆”,则( )A、事件A与B相互独立 B、事件A与C为互斥事件 C、 D、
二、多选题
-
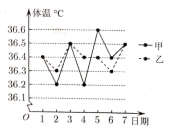
9. 新冠肺炎疫情防控期间,进出小区、超市、学校等场所,我们都需要先进行体温检测.某学校体温检测员对一周内甲,乙两名同学的体温进行了统计,其结果如图所示,则下列结论正确的是( )
 A、乙同学体温的极差为 B、甲同学体温的第三四分位数为 C、甲同学的体温比乙同学的体温稳定 D、乙同学体温的众数,中位数,平均数都相等10. 已知函数的部分图象如图,则( )
A、乙同学体温的极差为 B、甲同学体温的第三四分位数为 C、甲同学的体温比乙同学的体温稳定 D、乙同学体温的众数,中位数,平均数都相等10. 已知函数的部分图象如图,则( )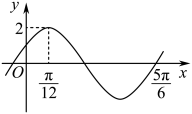 A、函数解析式 B、将函数的图象向左平移个单位长度可得函数的图象 C、直线是函数图象的一条对称轴 D、函数在区间上的最小值为11. 设圆 , 直线 , P为l上的动点过点P作圆O的两条切线 , 切点为A,B,则下列说法中正确的是( )A、直线l与圆O相交 B、的取值范围为 C、存在点P,使四边形为正方形 D、当点P坐标为时,直线的方程为12. 如图,棱长为2的正方体中,动点P满足 . 则以下结论正确的为( )
A、函数解析式 B、将函数的图象向左平移个单位长度可得函数的图象 C、直线是函数图象的一条对称轴 D、函数在区间上的最小值为11. 设圆 , 直线 , P为l上的动点过点P作圆O的两条切线 , 切点为A,B,则下列说法中正确的是( )A、直线l与圆O相交 B、的取值范围为 C、存在点P,使四边形为正方形 D、当点P坐标为时,直线的方程为12. 如图,棱长为2的正方体中,动点P满足 . 则以下结论正确的为( )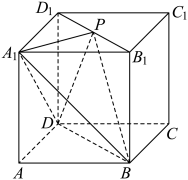 A、 , 使直线面 B、直线与面所成角的正弦值为 C、 , 三棱锥体积为定值 D、当时,三棱锥的外接球表面积为
A、 , 使直线面 B、直线与面所成角的正弦值为 C、 , 三棱锥体积为定值 D、当时,三棱锥的外接球表面积为三、填空题
-
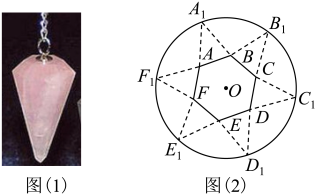
13. 的展开式中的系数为.(用数字作答)14. 若向量在向量上的投影向量为 , 且 , 则数量积 .15. 已知双曲线右焦点为 , 点P,Q在双曲线上,且关于原点O对称.若 , 且的面积为4,则双曲线的离心率 .16. 2022年12月3日,南昌市出士了东汉六棱锥体水晶珠灵摆吊坠如图(1)所示.现在我们通过DIY手工制作一个六棱锥吊坠模型.准备一张圆形纸片,已知圆心为O,半径为 , 该纸片上的正六边形的中心为为圆O上的点,如图(2)所示.分别是以为底边的等腰三角形.沿虚线剪开后,分别以为折痕折起 , 使重合,得到六棱锥,则当六棱锥体积最大时,底面六边形的边长为 .
四、解答题
-
17. 已知的内角A,B,C所对的边分别为a,b,c; , 且边 ,(1)、求的周长;(2)、若角 , 求的面积.18. 已知数列的前n项和为 , 且 , ____.请在①;②成等比数列;③ , 这三个条件中任选一个补充在上面题干中,并解答下面问题.
注:如果选择多个条件分别解答,按第一个解答计分..
(1)、求数列的通项公式;(2)、若 , 求数列的前n项和 .19. 如图1,直角梯形中, , E为的中点,现将沿着折叠,使 , 得到如图2所示的几何体,其中F为的中点,G为上一点,与交于点O,连接 .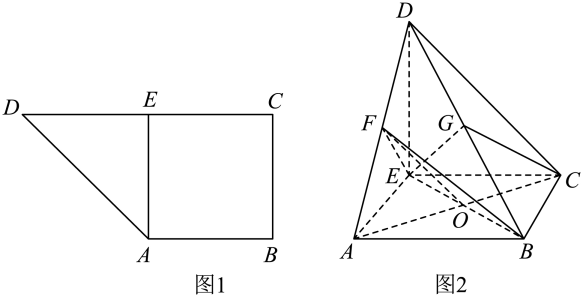 (1)、求证:平面;(2)、若面 , 求平面与平面的夹角 .20. 皮影戏是一种民间艺术,是我国民间工艺美术与戏曲巧妙结合而成的独特艺术品种,已有千余年的历史.而皮影制作是一项复杂的制作技艺,要求制作者必须具备扎实的绘画功底和高超的雕刻技巧,以及持之以恒的毅力和韧劲.每次制作分为画图与剪裁,雕刻与着色,刷清与装备三道主要工序,经过以上工序处理之后,一幅幅形态各异,富有神韵的皮影在能工巧匠的手里浑然天成,成为可供人们欣赏和操纵的富有灵气的影人.小李对学习皮影制作产生极大兴趣,师从名师勒学苦练,目前水平突飞猛进,三道主要工序中每道工序制作合格的概率依次为 , 三道序彼此独立,只有当每道工序制作都合格才为一次成功的皮影制作,该皮影视为合格作品.
(1)、求证:平面;(2)、若面 , 求平面与平面的夹角 .20. 皮影戏是一种民间艺术,是我国民间工艺美术与戏曲巧妙结合而成的独特艺术品种,已有千余年的历史.而皮影制作是一项复杂的制作技艺,要求制作者必须具备扎实的绘画功底和高超的雕刻技巧,以及持之以恒的毅力和韧劲.每次制作分为画图与剪裁,雕刻与着色,刷清与装备三道主要工序,经过以上工序处理之后,一幅幅形态各异,富有神韵的皮影在能工巧匠的手里浑然天成,成为可供人们欣赏和操纵的富有灵气的影人.小李对学习皮影制作产生极大兴趣,师从名师勒学苦练,目前水平突飞猛进,三道主要工序中每道工序制作合格的概率依次为 , 三道序彼此独立,只有当每道工序制作都合格才为一次成功的皮影制作,该皮影视为合格作品.(参考公式 , , 参考数据:).
(1)、求小李进行3次皮影制作,恰有一次合格作品的概率;(2)、若小李制作15次,其中合格作品数为X,求X的数学期望与方差;(3)、随着制作技术的不断提高,小李制作的皮影作品被某皮影戏剧团看中,聘其为单位制作演出作品,决定试用一段时间,每天制作皮影作品,其中前7天制作合格作品数y与时间:如下表:(第1天用数字1表示)时间(t)
1
2
3
4
5
6
7
合格作品数(y)
3
4
3
4
7
6
8
其中合格作品数(y)与时间(t)具有线性相关关系,求y关于t的线性回归方程(精确到0.01),并估算第15天能制作多少个合格作品(四舍五入取整)?