湖北省武汉市江岸区2022-2023学年高三上学期数学元月调考试卷
试卷更新日期:2023-02-06 类型:期末考试
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 是虚数单位,设复数满足 , 则的共轭复数对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间.紫砂壶的壶型众多,经典的有西施壶、掇球壶、石瓢壶、潘壶等.其中石瓢壶的壶体可以近似看成一个圆台,如图给出了一个石瓢壶的相关数据(单位:cm),现在向这个空石瓢壶中加入(约)的矿泉水后,问石瓢壶内水深约( )cm
 A、2.8 B、2.9 C、3.0 D、3.14. 已知定义在上的函数是奇函数且满足 , , 则( )A、 B、0 C、2 D、35. 已知 , , , 则 , , 的大小关系为( )A、 B、 C、 D、6. 双曲线的中心为原点 , 焦点在轴上,两条渐近线分别为 , , 经过右焦点垂直于的直线分别交 , 于 , 两点.已知、、成等差数列,且与反向.则双曲线的离心率为( )A、 B、 C、 D、7. 设和是函数在区间上的两个不同的值,当的值最小时,( )A、1 B、 C、 D、8. 已知圆锥的底面圆半径为 , 圆锥内部放有半径为1的球,球与圆锥的侧面和底面都相切,若 , 则圆锥体积的取值范围是( )A、 B、 C、 D、
A、2.8 B、2.9 C、3.0 D、3.14. 已知定义在上的函数是奇函数且满足 , , 则( )A、 B、0 C、2 D、35. 已知 , , , 则 , , 的大小关系为( )A、 B、 C、 D、6. 双曲线的中心为原点 , 焦点在轴上,两条渐近线分别为 , , 经过右焦点垂直于的直线分别交 , 于 , 两点.已知、、成等差数列,且与反向.则双曲线的离心率为( )A、 B、 C、 D、7. 设和是函数在区间上的两个不同的值,当的值最小时,( )A、1 B、 C、 D、8. 已知圆锥的底面圆半径为 , 圆锥内部放有半径为1的球,球与圆锥的侧面和底面都相切,若 , 则圆锥体积的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知正方体 , 点是上一点(不包括端点),则( )A、直线与所成的角为90° B、直线与所成的角为90° C、直线与所成的角为90° D、直线与平面所成的角为90°10. 等比数列的前项和为 , 前项的积 , 且 , , 则下列选项中成立的是( )A、对任意正整数 , B、 C、数列一定是等比数列 D、11. 设函数 , 若在[0,2π]有且仅有5个零点,则( )A、在(0,2π)有且仅有3个极大值点 B、在(0,2π)有且仅有2个极小值点 C、在(0,)单调递增 D、的取值范围是[ , )12. 已知函数 , 则下列选项正确的是( )A、在上单调递减 B、恰有一个极大值和一个极小值 C、当或时,有一个实数解 D、当时,有一个实数解
三、填空题
-
13. 在的展开式中,的系数为 .14. 已知正八边形的边长为2,是正八边形边上任意一点,则的最大值为.15. 已知抛物线的焦点为 , 过点的直线与相交于、两点(点位于第一象限),与的准线交于点,为线段的中点,过抛物线上点的直线与抛物线相切,且与直线平行,则的面积是.16. 对任意正实数 , 记函数在上的最小值为 , 函数在上的最大值为 , 若 , 则的所有可能值.
四、解答题
-
17. 已知中, , , 的对边 , , 成等比数列, , 延长至点 , 使.求:(1)、的大小;(2)、的取值范围.18. 在数列 , 中, , 对任意 , , 等差数列及正整数满足 , , 且.(1)、求数列 , 的通项公式;(2)、令 , 求前项和.19. 袋中有大小形状完全相同的3个白球,2个黄球,1个红球.现从袋中有放回的取球,每次随机取一个,直到红球出现3次,则停止取球,用表示取球停止时取球的次数.(1)、求和;(2)、设 , 求数学期望.20. 在如图所示的多面体中,四边形为正方形,A, , , 四点共面,且和均为等腰直角三角形,.平面平面 , .
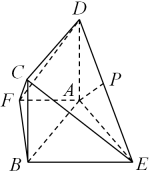 (1)、求多面体体积;(2)、若点在直线上,求与平面所成角的最大值.
(1)、求多面体体积;(2)、若点在直线上,求与平面所成角的最大值.