陕西省汉中市宁强县2022-2023学年九年级上学期期末测试数学试卷

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，共24.0分。）

1. 若 $\sqrt{a}$ 是最简二次根式，则a的值可能是（）

A、-2 B、2 C、 $\frac{3}{2}$ D、8

查看试题解析
2. 下列方程中，是一元二次方程的是（）

A、 $\frac{1}{x^{2}} + x - 1 = 0$ B、 $3 x + 1 = 5 x + 4^{2}$ C、 $a x^{2} + b x + c = 0$ D、 $m^{2} - 2 m + 1 = 0$

查看试题解析
3. 从如图所示的扑克牌中任取一张，牌面数字是3的倍数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. “翻开苏科版数学八年级下册，恰好翻到第20页”，这个事件是（）

A、必然事件 B、随机事件 C、不可能事件 D、确定事件

查看试题解析
5. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x + \frac{1}{2} = 0$ 有实数根，则实数 $k$ 的取值范围是（）

A、 $k \leq 2$ B、 $k < 2$ C、 $k < 2$ 且 $k \neq 0$ D、 $k \leq 2$ 且 $k \neq 0$

查看试题解析
6. 按如图所示的运算程序，能使输出的y值为 $\frac{1}{2}$ 的是（）

A、α=60°，β=45° B、α=30°，β=45° C、α=30°，β=30° D、α=45°，β=30°

查看试题解析
7. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， $A B + B C = 12 c m$ ，则 $A B$ 的长度为（）

A、 $6 c m$ B、 $7 c m$ C、 $8 c m$ D、 $9 c m$

查看试题解析
8. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，该图象过点 $A (- 5 ， 0)$ ，对称轴为直线 $x = - 2$ ，下列结论：① $a b c < 0$ ；② $4 a - 2 b + c > 0$ ；③若 $B (- 3 ， y_{1})$ 与 $C (- 4 ， y_{2})$ 是抛物线上两点，则 $y_{2} > y_{1}$ ；④ $5 a + c = 0$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共5小题，共15.0分）

9. 计算 $\sqrt{20} \cdot \sqrt{\frac{1}{5}}$ 的结果．

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别在边 $A B$ ， $B C$ 上， $D E / / A C$ ，若 $D B = 4$ ， $D A = 2$ ， $D E = 3$ ，则 $A C =$ .

查看试题解析
11. 如果方程x²＋4x＋n＝0可以配方成（x＋m）²-3＝0，那么（n-m）²⁰²⁰＝．

查看试题解析
12. 如图，在边长相同的小正方形组成的网格中，点 $A$ 、 $B$ 、 $C$ 、 $D$ 都在这些小正方形的顶点上，线段 $A B$ 、 $C D$ ，相交于点 $P$ ，则 $\tan ∠ A P D$ 的值是．

查看试题解析
13. 已知如图， $D E$ 是 $Δ A B C$ 的中位线，点 $P$ 是 $D E$ 的中点， $C P$ 的延长线交 $A B$ 于点A $Q$ ，那么 $S_{Δ C P E} ： S_{Δ A B C}$ = ．

查看试题解析

三、解答题（本大题共13小题，共81.0分。）

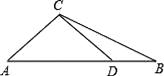
14. 计算： $| 1 - \sqrt{3} | - \sqrt{12} + {(π - 3)}^{0} + \sqrt{{(- 3)}^{2}} + \tan 60 °$ ．

查看试题解析
15. 用公式法解方程： $4 x^{2} + x - 3 = 0$ ．

查看试题解析
16. 如图，在∠ABC中，∠B=30°，AC= $\sqrt{2}$ ，等腰直角△ACD斜边AD在AB边上，求BC的长．

查看试题解析
17. 图①、图②、图③都是 $5 \times 4$ 的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长为1，点A、B、C、D均在格点上．请按要求解答问题．（画图只能用无刻度的直尺，保留作图痕迹）要求：

(1)、如图①， $\frac{B E}{C E} =$ ；

(2)、如图②，在BC上找一点F使 $B F = 2$ ；

(3)、如图③，在AC上找一点M，连接BM、DM，使 $△ A B M ∽ △ C D M$ ．

查看试题解析
18. 关于x的一元二次方程x²+（m+4）x﹣2m﹣12＝0，求证：

(1)、方程总有两个实数根；

(2)、如果方程的两根相等，求此时方程的根.

查看试题解析
19. 如图，小亮父亲想用长为 $80 m$ 的栅栏，再借助房屋的外墙围成一个矩形羊圈 $A B C D$ ，已知房屋外墙长 $50 m$ ，设矩形 $A B C D$ 的边 $A B = x m$ ，面积为 $S m^{2}$ ．

(1)、写出S与x之间的关系式，并指出x的取值范围；

(2)、当 $A B ， B C$ 分别为多少米时，羊圈的面积最大？最大面积是多少？

查看试题解析
20. 新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有121人患病，设每轮传染中平均一个人传染了多少个人？

查看试题解析
21. 已知： $△ A B C$ 在直角坐标平面内，三个顶点的坐标分别为 $A (0 ， 3)$ 、 $B (3 ， 4)$ 、 $C (2 ， 2)$ （正方形网格中每个小正方形的边长是一个单位长度）．

( 1 )在网格内画出 $△ A B C$ 关于 $x$ 轴的轴对称图形 $△ A_{1} B_{1} C_{1}$ ，则点 $C_{1}$ 的坐标为（▲ ， ▲ ）；

( 2 )以点B为位似中心，在网格内画出 $△ A_{2} B_{2} C_{2}$ ，使 $△ A_{2} B_{2} C_{2}$ 与 $△ A B C$ 位似，且位似比为2：1；则点 $C_{2}$ 的坐标为（▲ ， ▲ ）．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 、 $E$ 分别在 $B C$ 、 $A C$ 上，且 $D C = D E$ ．

(1)、求证： $△ A B C ∽ △ D E C$ ；

(2)、若 $A B = 5$ ， $A E = 1$ ， $D E = 3$ ，求 $B C$ 的长．

查看试题解析
23. 如图是 $G 5$ 高速公路边水平地面上的交通警示牌，已知警示牌 $C D$ 的高为 $(4 \sqrt{3} - 5)$ 米， $A B = 7$ 米， $∠ M A D = 45 °$ ， $∠ M B C = 30 °$ ，求 $D M$ 的高度．

查看试题解析
24. 小明和小芳做配紫色游戏，如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，

(1)、利用列表或树状图的方法表示此游戏所有可能出现的结果；

(2)、若出现紫色，则小明胜．此游戏的规则对小明、小芳公平吗？试说明理由．

查看试题解析
25. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于点 $A (1 ， 0)$ 和点 $B (- 3 ， 0)$ ，与y轴交于点 $C (0 ， 3)$ ．

(1)、求拋物线的解析式；

(2)、设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使 $△ C M P$ 为等腰三角形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
26. 如图， $△ A B C$ 中， $∠ B A C = 120 °$ ， $A B = A C$ ，点 $D$ 为 $B C$ 边上一点．

(1)、如图1，若 $A D = A M$ ， $∠ D A M = 120 °$ ．
①求证： $B D = C M$ ；

②若 $∠ C M D = 90 °$ ，求 $\frac{B D}{C D}$ 的值．

(2)、如图2，点 $E$ 为线段 $C D$ 上一点，且 $C E = 4$ ， $A B = 6 \sqrt{3}$ ， $∠ D A E = 60 °$ ，求 $D E$ 的长．

查看试题解析