陕西省延安市宝塔区2022-2023学年七年级上学期期末数学试卷

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、选择题（共16小题，1-10题，每题3分，11-16题，每题2分，共42分）

1. -12的相反数是（）

A、12 B、 $\frac{1}{12}$ C、- $\frac{1}{12}$ D、-12

查看试题解析
2. 下列各图中，表示“线段 $C D$ ”的是（）

A、 B、 C、 D、

查看试题解析
3. 世界文化遗产—长城的总长约为210000米，数据210000用科学记数法可表示为（）

A、0.21×10⁷ B、2.1×10⁵ C、2.1×10⁶ D、21×10⁵

查看试题解析
4. 如图，射线 $O A$ 表示的方向是（）

A、北偏东 $65 °$ B、北偏西 $35 °$ C、南偏东 $65 °$ D、南偏西 $35 °$

查看试题解析
5. 如图，正方体表面展开平面图中六个面分别标注有“战、胜、新、冠、病、毒”六个中文，在原正方体中“冠”的对面是（）

A、毒 B、新 C、胜 D、冠

查看试题解析
6. 要调查下列问题，适合采用全面调查（普查）的是（）

A、中央电视台《开学第一课》的收视率 B、某市中学生学习“四史”，做红色接班人活动情况统计 C、即将发射的气象卫星的零部件质量 D、某品牌新能源汽车的最大续航里程

查看试题解析
7. 下列变形中，运用等式的性质变形不正确的是（）

A、若x＝y，则x+3＝y+3 B、若x＝y，则-4x＝-4y C、若x＝y，则ax＝ay D、若x＝y，则 $\frac{x}{a} = \frac{y}{a}$

查看试题解析
8. 单项式-2πx³yz的系数和次数分别是（）

A、-2，6 B、-2π，5 C、-2，7 D、-2π，6

查看试题解析
9. 已知方程（m-3）x^|m|^-²＝18是关于x的一元一次方程，则m的值是（）

A、2 B、3 C、±3 D、-3

查看试题解析
10. 若x＝2是关于x的方程2x+a＝0的解，则a的值为（）

A、-4 B、-2 C、4 D、2

查看试题解析
11. 如图是由一副三角尺拼成的图案，它们有公共顶点O，且有一部分重叠，已知∠BOD＝30°，则∠AOC的度数是（）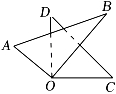

A、40° B、120° C、140° D、150°

查看试题解析
12. 是中国古代数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木头，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余一尺，问木头长多少尺？可设木头长为x尺，则所列方程正确的是（）

A、（x+4.5）-2x＝1 B、2x-（x+4.5）＝1 C、 $x - \frac{x + 4.5}{2} = 1$ D、 $\frac{x + 4.5}{2} - x = 1$

查看试题解析
13. 下列语句正确的个数是（）
①两条射线组成的图形叫做角；②反向延长线段AB得到射线BA；③延长射线OA到点C；④若AB＝BC，则点B是AC中点；⑤连接两点的线段叫做两点间的距离；⑥两点之间直线最短．

A、1 B、2 C、3 D、4

查看试题解析
14. 实数在数轴上的位置如图所示，则下列各式正确的是（）

A、a+b＞0 B、a-b＜0 C、ab＞0 D、|b|＞a

查看试题解析
15. 如图，在正方形 $A B C D$ 中，E 为 $D C$ 边上一点，沿线段 $B E$ 对折后，若 $∠ A B F$ 比 $∠ E B F$ 大 $18 °$ ，则 $∠ E B C$ 的度数是（）

A、24度 B、20度 C、26度 D、30度

查看试题解析
16.
如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（）根火柴．

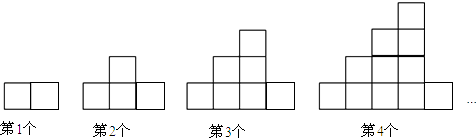A、156 B、157 C、158 D、159

查看试题解析

二、填空题（本小题3个小题，每空3分，共9分）

17. 五边形的对角线一共有条.

查看试题解析
18. 计算：22°11′50″+10°13′20″＝．（结果化成度、分、秒的形式）

查看试题解析
19. 已知线段 $A B$ 长 $8 c m$ ，在直线 $A B$ 上有一点 C，且 $A B = 4 B C$ ，则 $A C$ 的长为cm．

查看试题解析

三、解答题（20题每小题12分，共12分；21题6分；22题6分；23题7分；24题8分；25题10分，共49分）

20. 计算：

(1)、（-3.2）+12.5+（-26.8）-（-3.5）．

(2)、解方程： $\frac{2 x - 1}{3} - \frac{x - 2}{6} = 2$

(3)、化简，再求值：2x²y+8xy-2（3xy-2x²y）-3xy，其中x＝-1，y＝2．

查看试题解析
21. 某学校计划在八年级开设“折扇”“刺绣”“剪纸”“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程，为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图所示的条形统计图和扇形统计图．（部分信息未给出）

请你根据以上信息解决下列问题：

(1)、参加问卷调查的学生人数为▲ 名，补全条形统计图（画图并标注相应数据）；

(2)、“陶艺”课程所对应的扇形圆心角的度数是多少？

(3)、若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？

查看试题解析
22. 如图，点A、O、B在同一直线上，OC平分∠AOB，若∠COD＝28°．

(1)、求∠BOD的度数；

(2)、若OE平分∠BOD，求∠COE的度数．

查看试题解析
23. 某商场从厂家批发电视机进行零售，批发价格与零售价格如表：
电视机型号
甲
乙
批发价（元/台）
1500
2500
零售价（元/台）
2500
4000
若商场购进甲、乙两种型号的电视机共50台，用去10万元．

(1)、求商场购进甲、乙型号的电视机各多少台？

(2)、迎“新年”商场决定进行优惠促销：以零售价的七五折销售乙种型号电视机，两种电视机销售完毕，商场共获利15%，求甲种型号电视机打几折销售？

查看试题解析
24. 如图，已知线段AD上有两个定点B，C．

(1)、图中共有条线段．

(2)、若在线段CD上增加一点，则增加了条线段．

(3)、现有一列往返于A，B两地的火车，中途停靠4个站．问：①有种票价；②要准备种车票．

(4)、已知A，B两地之间相距160km，在A，B所在的公路（AB看成直线）上有一处C，且B与C之间的距离为30km，M在A，C两地的正中间，求M与A地之间的距离．

查看试题解析
25. 如图

(1)、如图1：正方形ABCD边长为6，点P、点Q在正方形的边上．点P从点A以每秒3个单位长度的速度沿A→B→C→D→A折线循环运动，同时点Q从点C以每秒1个单位长度的速度沿C→D→A→B→C折线循环运动．设点P运动时间为x秒．①当点P在AB上运动时，PA＝当点Q在CD运动时CQ＝（用含x的代数式表示）；②当x为何值时，点P和点Q第一次相遇．

(2)、如图2：是长为8，宽为4的长方形ABCD，点E为边CD的中点，点M从点A以每秒2个单位长度的速度沿A→B→C折线运动，到达点C停止．设点M运动时间为t秒，当三角形AME的面积等于8时，请求出t的值．

查看试题解析

电视机型号	甲	乙
批发价（元/台）	1500	2500
零售价（元/台）	2500	4000