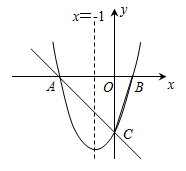贵州省黔南州长顺县2022-2023学年九年级上学期段考数学试卷(三)
试卷更新日期:2023-02-06 类型:期末考试
一、选择题(本题共12小题,共36分)
-
1. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列4个说法中,正确的有( )
2. 下列4个说法中,正确的有( )①直径是弦 ②弦是直径 ③任何一条直径所在的直线都是圆的对称轴 ④弧是半圆
A、1个 B、2个 C、3个 D、4个3. 下列说法正确的是( )A、一个袋中装有3个红球、5个白球,任意摸出一个球是红球的概率是 B、某彩票的中奖概率是5%,那么买100张彩票一定有张中奖 C、射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是 D、小李与小陈做猜拳游戏,规定每人每次出一只手,且至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,则小李获胜的可能性较大4. 下列说法中,正确的是( )A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、直径未必是弦5. 如图,在中,是直径,是弦,连接 , 若 , 则的度数是( ) A、 B、 C、 D、6. 如图的直径垂直于弦 , 垂足为 , 且 , , 则的半径为( )
A、 B、 C、 D、6. 如图的直径垂直于弦 , 垂足为 , 且 , , 则的半径为( ) A、 B、 C、 D、7. 用如图所示的两个转盘分别进行四等分和三等分 , 设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计 , 若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( )
A、 B、 C、 D、7. 用如图所示的两个转盘分别进行四等分和三等分 , 设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计 , 若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( ) A、 B、 C、 D、8. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A、 B、 C、 D、8. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )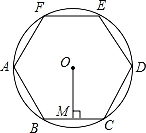 A、2 B、 C、2 D、29. 二次函数与一次函数在同一坐标系中的大致图象是( )A、
A、2 B、 C、2 D、29. 二次函数与一次函数在同一坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、 10. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )
10. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )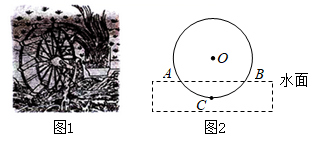 A、1米 B、 米 C、2米 D、 米11. 如图,在长为32米、宽为12米的矩形地面上修建如图所示的道路(图中的阴影部分)余下部分铺设草坪,要使得草坪的面积为300平方米,则可列方程为( )
A、1米 B、 米 C、2米 D、 米11. 如图,在长为32米、宽为12米的矩形地面上修建如图所示的道路(图中的阴影部分)余下部分铺设草坪,要使得草坪的面积为300平方米,则可列方程为( ) A、 B、 C、 D、12. 如图,已知抛物线交轴于点和轴正半轴于点 , 且 , 交轴正半轴于点有下列结论:;;时有最大值;其中,正确结论的个数是( )
A、 B、 C、 D、12. 如图,已知抛物线交轴于点和轴正半轴于点 , 且 , 交轴正半轴于点有下列结论:;;时有最大值;其中,正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本题共4小题,共16分)
-
13. 如图,点 , 点 , 点在上,分别连接 , , 若 , , 则 .
 14. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.
14. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.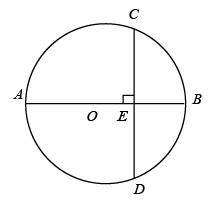 15. 二次函数的部分图象如图所示,则方程的根为 .
15. 二次函数的部分图象如图所示,则方程的根为 .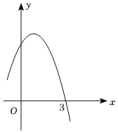 16. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心 , 则折痕的长为 .
16. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心 , 则折痕的长为 .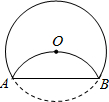
三、解答题(本题共9小题,共98分)
-
17. 如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
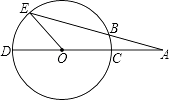 (1)、求∠AOB的度数.(2)、求∠EOD的度数.18. 某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本y(万元)与产品数量x(件)之间具有函数关系y=ax2+bx.当x=10时,y=400;当x=20时,y=1000.B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?19. 如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)、求∠AOB的度数.(2)、求∠EOD的度数.18. 某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本y(万元)与产品数量x(件)之间具有函数关系y=ax2+bx.当x=10时,y=400;当x=20时,y=1000.B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?19. 如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF. (1)、求证:;(2)、若AD=BE=2,求BF的长.20. 高致病性禽流感是一种传染性极强的传染病.(1)、养殖场有4万只鸡假设有一只鸡得了禽流感,如果不采取任何措施,那么第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依此类推,请问到第四天,共有多少只鸡得了禽流感?到第几天,所有的鸡都会感染禽流感?(2)、为防止禽流感蔓延,防疫部门规定,离疫点3千米范围内为捕杀区所有的禽类全部捕杀离疫点千米范围内为免疫区,所有的禽类强制免疫;同时对捕杀区和免疫区的村庄,道路实行全封闭管理现有一条笔直的公路通过禽流感病区如图所示,为疫点,到公路的最短距离为1千米,问这条公路在该免疫区内有多少千米?结果保留根号
(1)、求证:;(2)、若AD=BE=2,求BF的长.20. 高致病性禽流感是一种传染性极强的传染病.(1)、养殖场有4万只鸡假设有一只鸡得了禽流感,如果不采取任何措施,那么第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依此类推,请问到第四天,共有多少只鸡得了禽流感?到第几天,所有的鸡都会感染禽流感?(2)、为防止禽流感蔓延,防疫部门规定,离疫点3千米范围内为捕杀区所有的禽类全部捕杀离疫点千米范围内为免疫区,所有的禽类强制免疫;同时对捕杀区和免疫区的村庄,道路实行全封闭管理现有一条笔直的公路通过禽流感病区如图所示,为疫点,到公路的最短距离为1千米,问这条公路在该免疫区内有多少千米?结果保留根号 21. 如图,是的直径,点和点是上的两点,过点作的切线交延长线于点 .
21. 如图,是的直径,点和点是上的两点,过点作的切线交延长线于点 . (1)、若 , 求的度数;(2)、若 , , 求半径的长.22. 如图,为的外接圆,为的直径,点为的中点,连接 .
(1)、若 , 求的度数;(2)、若 , , 求半径的长.22. 如图,为的外接圆,为的直径,点为的中点,连接 . (1)、求证:;(2)、设交于 , 若 , 求阴影部分面积.23. 如图,抛物线的图象交轴于 , 两点,交轴于点 , 直线经过 , 两点.
(1)、求证:;(2)、设交于 , 若 , 求阴影部分面积.23. 如图,抛物线的图象交轴于 , 两点,交轴于点 , 直线经过 , 两点. (1)、求抛物线的解析式;(2)、点为抛物线第一象限上的一动点,连接 , , 求面积的最大值,并求出此时点的坐标.
(1)、求抛物线的解析式;(2)、点为抛物线第一象限上的一动点,连接 , , 求面积的最大值,并求出此时点的坐标.