贵州省安顺市六校联考2022-2023学年九年级上学期期末数学试卷
试卷更新日期:2023-02-06 类型:期末考试
一、选择题(共12题,每小题5分,共60分)
-
1. 已知关于x的一元二次方程mx2﹣(m+2)x+ =0有两个不相等的实数根x1 , x2.若 + =4m,则m的值是( )A、2 B、﹣1 C、2或﹣1 D、不存在2. 已知2是关于x的方程x2﹣2mx+3m=0的一个根, 并且这个方程的两个根恰好是等腰三角形ABC的两条边长, 则三角形ABC的周长为( )
A、10 B、14 C、10或14 D、8或103. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=- . 下列结论中,正确的是( ) A、abc>0 B、a+b=0 C、2b+c>0 D、4a+c<2b4. 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m , 则水面下降1m时,水面宽度增加( )
A、abc>0 B、a+b=0 C、2b+c>0 D、4a+c<2b4. 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m , 则水面下降1m时,水面宽度增加( ) A、1m B、2m C、(2 ﹣4)m D、( ﹣2)m5. 如图,△ABC中,AB=4,AC=3,BC=2,将△ABC绕点A顺时针旋转60°得到△AED,则BE的长为( )
A、1m B、2m C、(2 ﹣4)m D、( ﹣2)m5. 如图,△ABC中,AB=4,AC=3,BC=2,将△ABC绕点A顺时针旋转60°得到△AED,则BE的长为( ) A、5 B、4 C、3 D、26. 已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )A、a=5,b=1 B、a=﹣5,b=1 C、a=5,b=﹣1 D、a=﹣5,b=﹣17. 如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=6,则△PCD的周长为( )
A、5 B、4 C、3 D、26. 已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )A、a=5,b=1 B、a=﹣5,b=1 C、a=5,b=﹣1 D、a=﹣5,b=﹣17. 如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=6,则△PCD的周长为( )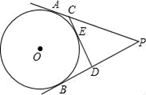 A、8 B、6 C、12 D、108. 如图,正五边形 内接于⊙ , 为 上的一点(点 不与点 重合),则 的度数为( )
A、8 B、6 C、12 D、108. 如图,正五边形 内接于⊙ , 为 上的一点(点 不与点 重合),则 的度数为( ) A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2 , 则阴影部分的面积为( )
A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2 , 则阴影部分的面积为( ) A、 B、π C、2π D、4π10. 下列事件中,必然事件是( )A、抛掷 枚质地均匀的骰子,向上的点数为 B、两直线被第三条直线所截,同位角相等 C、抛一枚硬币,落地后正面朝上 D、实数的绝对值是非负数11. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,矩形ABCD内的一个动点P落在阴影部分的概率是( )
A、 B、π C、2π D、4π10. 下列事件中,必然事件是( )A、抛掷 枚质地均匀的骰子,向上的点数为 B、两直线被第三条直线所截,同位角相等 C、抛一枚硬币,落地后正面朝上 D、实数的绝对值是非负数11. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,矩形ABCD内的一个动点P落在阴影部分的概率是( )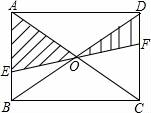 A、 B、 C、 D、12. 小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体,…按照此规律,从第(100)个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是( )
A、 B、 C、 D、12. 小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体,…按照此规律,从第(100)个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6题,每小题5分,共30分)
-
13. 设x1、x2是方程5x2﹣3x﹣2=0的两个实数根,则 的值为 .14. 若实数m,n满足m+n= mn,且n≠0时,就称点P(m, )为“完美点”,若反比例函数y= 的图象上存在两个“完美点”A,B,且AB= ,则k的值为.15. 如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是 .
 16. 如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1 , 当C1D1第一次经过顶点C时,旋转角∠ABA1= .
16. 如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1 , 当C1D1第一次经过顶点C时,旋转角∠ABA1= .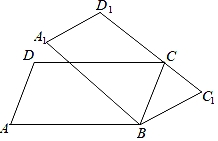 17. 如图,正方形ABCD的边长为4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是 .
17. 如图,正方形ABCD的边长为4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是 . 18. 若自然数n使得三个数的竖式加法运算“n+(n+1)+(n+2)”产生进位现象,则称n为“连加进位数”.例如,2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;51是“连加进位数”,因为51+52+53=156产生进位现象.如果从0,1,…,99这100个自然数中任取一个数,那么取到“连加进位数”的概率是 .
18. 若自然数n使得三个数的竖式加法运算“n+(n+1)+(n+2)”产生进位现象,则称n为“连加进位数”.例如,2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;51是“连加进位数”,因为51+52+53=156产生进位现象.如果从0,1,…,99这100个自然数中任取一个数,那么取到“连加进位数”的概率是 .三、解答题(共5题,共60分)
-
19. 设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2 ,(1)、若x12+x22=6,求m值;(2)、求 的最大值.20. 如图,已知抛物线y=+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点 E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.21. 如图,在△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,连接AD、BD,将△BAD绕点A按逆时针方向旋转到△CAE的位置,连接DE.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点 E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.21. 如图,在△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,连接AD、BD,将△BAD绕点A按逆时针方向旋转到△CAE的位置,连接DE. (1)、若AD=1,求DE的长;(2)、连接CD,若F、G、H分别为BC、CD、DE的中点,连接GF、GH,求证:GH=GF.22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)、若AD=1,求DE的长;(2)、连接CD,若F、G、H分别为BC、CD、DE的中点,连接GF、GH,求证:GH=GF.22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC. (1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求的长.23. 为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区 户家庭的月用水量,绘制了下面不完整的统计图.
(1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求的长.23. 为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区 户家庭的月用水量,绘制了下面不完整的统计图.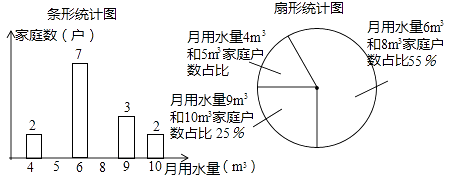 (1)、求 并补全条形统计图;(2)、求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;(3)、从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.
(1)、求 并补全条形统计图;(2)、求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;(3)、从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.