贵州省安顺市六校联考2022-2023学年八年级上学期期末数学试卷

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，共60.0分。）

1. 如果等腰三角形两边长是8cm和4cm，那么它的周长是（）

A、20cm B、16cm C、20cm或16cm D、12cm

查看试题解析
2. 如图，在△ABC中，∠ABC=40°，∠ACD=76°，BE平分∠ABC，CE平分△ABC的外角∠ACD，则∠E=（）

A、40° B、36° C、20° D、18°

查看试题解析
3. 如图，△ABC≌△DCB，若AC=7，BE=5，则DE的长为（）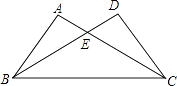

A、2 B、3 C、4 D、5

查看试题解析
4. 如图， $AC = CD$ ， $∠ B = ∠ E = 90 °$ ， $AC ⊥ CD$ ，则不正确的结论是（）

A、 $∠ A$ 与 $∠ D$ 互为余角 B、 $∠ 1 = ∠ 2$ C、 $△ ABC$ ≌ $△ CED$ D、 $∠ A = ∠ 2$

查看试题解析
5. 如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S_△_ABO：S_△_BCO：S_△_CAO等于（）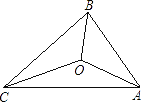

A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：5

查看试题解析
6. 如图，在平面直角坐标系中， $△ ABC$ 位于第二象限，点 $A$ 的坐标是 $(- 2 ， 3)$ ，先把 $△ ABC$ 向右平移4个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，再作与 $△ A_{1} B_{1} C_{1}$ 关于 $x$ 轴对称的 $△ A_{2} B_{2} C_{2}$ ，则点 $A$ 的对应点 $A_{2}$ 的坐标是（）

A、 $(- 3 ， 2)$ B、 $(2 ， - 3)$ C、 $(1 ， - 2)$ D、 $(- 1 ， 2)$

查看试题解析
7.
如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（　　）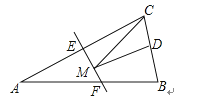

A、6 B、8 C、10 D、12

查看试题解析
8. 如 $(x + a)$ 与 $(x + 3)$ 的乘积中不含 $x$ 的一次项，则 $a$ 的值为（）

A、3 B、-3 C、1 D、-1

查看试题解析
9. 下列各式分解因式正确的是（）

A、 $2 a^{2} - 8 b^{2} = 2 (a + 4 b) (a - 4)$ B、 $x^{2} - 6 x + 9 = {(x - 3)}^{2}$ C、 $2 m^{2} - 4 mn + 9 n^{2} = {(2 m - 3 n)}^{2}$ D、 $x (x - y) + y (y - x) = (x - y) (x + y)$

查看试题解析
10. 已知二次三项式 $x^{2} - kx - 15$ 能分解成系数为整数的两个一次因式的积，则整数 $k$ 的取值范围有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 化简 $(\frac{m^{2}}{m - 2} + \frac{4}{2 - m}) \div (m + 2)$ 的结果是（）

A、0 B、1 C、-1 D、 ${(m + 2)}^{2}$

查看试题解析
12. 如果关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x - m}{3} \leq 1 \\ x - 4 > 3 (x - 2) \end{array}$ 的解集为 $x < 1$ ，且关于 $x$ 的分式方程 $\frac{2}{1 - x} + \frac{mx}{x - 1} = 3$ 有非负数解，则所有符合条件的整数 $m$ 的值之和是（）

A、-2 B、0 C、3 D、5

查看试题解析

二、填空题（本大题共5小题，共30.0分）

13. 等腰 $△ ABC$ 中， $AB = AC$ ， $BD$ 平分 $∠ ABC$ ，若 $∠ BDC = 120 °$ ，则 $∠ A =$ ．

查看试题解析
14. 若 $x^{2} + 2 (m + 3) x + 9$ 是关于 $x$ 的完全平方式，则 $m =$ ．

查看试题解析
15. 如图，等腰三角形 $ABC$ 的底边 $BC$ 长为 $4$ ，面积是 $16$ ，腰 $AC$ 的垂直平分线 $EF$ 分别交 $AC$ ， $AB$ 边于点 $E$ ， $F$ ，若点 $D$ 为 $BC$ 边的中点，点 $M$ 为线段 $EF$ 上一动点，则 $△ CDM$ 周长的最小值为．

查看试题解析
16. 已知n为整数，若一个三角形的三边长分别是 $4 n + 31$ ， $n - 13$ ，6n ，则所有满足条件的n值的和为．

查看试题解析
17. 对于代数式 $m$ ， $n$ ，定义运算“ $※$ ”： $m ※ n = \frac{m + n - 6}{mn} (mn \neq 0)$ ，例如： $4 ※ 2 = \frac{4 + 2 - 6}{4 \times 2} .$ 若 $(x - 1) ※ (x + 2) = \frac{A}{x - 1} + \frac{B}{x + 2}$ ，则 $2 A - B =$ ．

查看试题解析

三、解答题（本大题共5小题，共60.0分。）

18. 如图，在四边形 $ABCD$ 中， $AB / / CD$ ，点 $E$ 、 $F$ 分别在 $AD$ 、 $BC$ 边上，连接 $AC$ 交 $EF$ 于 $G$ ， $∠ 1 = ∠ BAC$ ．

(1)、求证： $EF / / CD$ ；

(2)、若 $∠ CAF = 15 °$ ， $∠ 2 = 45 °$ ， $∠ 3 = 20 °$ ，求 $∠ B$ 和 $∠ ACD$ 的度数．

查看试题解析
19. 如图， $D$ 、 $C$ 、 $F$ 、 $B$ 四点在一条直线上， $AB = DE$ ， $AC ⊥ BD$ ， $EF ⊥ BD$ ，垂足分别为点 $C$ 、点 $F$ ， $CD = BF$ ．

(1)、求证： $△ ABC$ ≌ $△ EDF$ ．

(2)、连结 $AD$ 、 $BE$ ，求证： $AD = EB$ ．

查看试题解析
20. 如图，在 $△ ABC$ 中，已知 $AB = AC$ ， $AD$ 是 $BC$ 边上的中线，点 $E$ 是 $AB$ 边上一动点，点 $P$ 是 $AD$ 上的一个动点．

(1)、若 $∠ BAD = 37 °$ ，求 $∠ ACB$ 的度数；

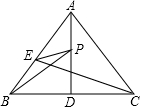(2)、若 $BC = 6$ ， $AD = 4$ ， $AB = 5$ ，且 $CE ⊥ AB$ 时，求 $CE$ 的长；

(3)、在（2）的条件下，请直接写出 $BP + EP$ 的最小值．

查看试题解析
21. 先化简，再求值：已知代数式 $(ax - 3) (2 x + 4) - x^{2} - b$ 化简后，不含有 $x^{2}$ 项和常数项．

(1)、求 $a$ 、 $b$ 的值；

(2)、求 $(b - a) (- a - b) + {(- a - b)}^{2} - a (2 a + b)$ 的值．

查看试题解析
22. 某班组织登山活动，同学们分甲乙两组从山脚下沿着一条道路同时向山顶进发．设甲乙两组行进同一段路所用的时间之比为2：3．

(1)、直接写出甲乙两组行进的速度之比．

(2)、当甲组到达山顶时，乙组行进到山腰A处，且A处离出顶的路程尚有1.2千米．试问山脚离山顶的路程有多远．

(3)、在题（2）的基础上，设乙组从A处继续登山，甲组再从原路下山，下山速度与上山速度相同，并且在山腰B处与乙组相遇．请你先根据以上情景提出一个相应的问题，再给予解答．（要求：①问题的提出不得再增添其他条件；②问题的解决必须利用上述情景提供的所有已知条件．）

查看试题解析