浙江省衢州市实验教育集团2022-2023学年九年级上学期期末考试数学试卷
试卷更新日期:2023-02-06 类型:期末考试
一、单选题
-
1. 若 ,则 的值是( )A、2 B、3 C、 D、2. 某几何体的三视图如图,则该几何体是( )
 A、长方体 B、正三棱柱主视图左视图 C、球 D、圆柱3. 将抛物线向左平移2个单位,所得抛物线是( )A、 B、 C、 D、4. 如图,将线段AB绕点O顺时针旋转90°得到线段 , 那么的对应点的坐标是( )
A、长方体 B、正三棱柱主视图左视图 C、球 D、圆柱3. 将抛物线向左平移2个单位,所得抛物线是( )A、 B、 C、 D、4. 如图,将线段AB绕点O顺时针旋转90°得到线段 , 那么的对应点的坐标是( ) A、 B、 C、 D、5. 如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )
A、 B、 C、 D、5. 如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( ) A、OE=m•tanα B、CD=2m•sinα C、AE=m•cosα D、S△COD=m2•sinα
A、OE=m•tanα B、CD=2m•sinα C、AE=m•cosα D、S△COD=m2•sinα二、填空题
-
6. 抛物线的对称轴是直线.7. 将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)挪一次,朝上一面的点数是3的概率是.8. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为 , 则它的宽为.(结果保留根号)9. 如图,在中, , 点I为三角形的重心,于点H,则cm.
 10. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.
10. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.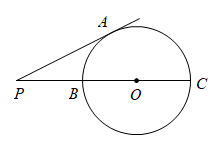
三、解答题
-
11. 计算:12. 已知:如图,C,D是以为直径的半圆周的三等分点,.求阴影部分的面积?
 13. 如图为某学校体育看台侧面的示意图,看台AC的坡比i为 , 看台高度为m,从顶棚的D处看E处的仰角 , 距离为5m,E处到看台底端A处的水平距离为3m(结果精确到m,参考数据:)
13. 如图为某学校体育看台侧面的示意图,看台AC的坡比i为 , 看台高度为m,从顶棚的D处看E处的仰角 , 距离为5m,E处到看台底端A处的水平距离为3m(结果精确到m,参考数据:) (1)、求的长.(2)、求的长.14. 根据以下素材,探索完成任务
(1)、求的长.(2)、求的长.14. 根据以下素材,探索完成任务如何设计纸盒
素材1
利用一边长为40cm的正方形纸板可能设计成如图1和图2所示的两种纸盒,图1是无盖的纸盒,图2是一个有盖的纸盒.

素材2
如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖的长方体盒子。

问题解决
任务1
初步探究:折一个底面积为无盖长方体盒子
求剪掉的小正方形的边长为多少?
任务2
探究折成的无盖长方体盒子的侧面积是否有最大值?
如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,说明理由
15. 综合实践课上,小慧用两张如图1所示的直角三角形纸片: , 斜边重合拼成四边形,接着在 , 上取点E,F,连 , , 使. (1)、若拼成的四边形如图2所示:则﹔(2)、如图3,连接对角线 , 相交于点O,分别交 , 于点G,H,若平分 ,
(1)、若拼成的四边形如图2所示:则﹔(2)、如图3,连接对角线 , 相交于点O,分别交 , 于点G,H,若平分 ,①判断的形状并说明理由.
② , 求的长.