广西壮族自治区贵港市港南区2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是负数的是（）

A、 $- \frac{2}{3}$ B、0 C、 $\frac{1}{2}$ D、1

查看试题解析
2. 已知x=5是方程ax﹣8=20+a的解，则a的值是（　　）

A、2 B、3 C、7 D、8

查看试题解析
3. 要调查下列问题，适合采用抽样调查的是（）

A、疫情期间，了解全校师生入校时体温情况 B、检测我国研制的C919大飞机的零件的质量 C、了解一批灯泡的使用寿命 D、了解小明某周每天参加体育运动的时间

查看试题解析
4. 已知∠α＝25°30'，则它的补角为（）

A、25°30′ B、64° 30' C、164° 30' D、154°30′

查看试题解析
5. 下列运用等式性质进行的变形中，正确的是（）

A、若 $a = b$ ，则 $a + 5 = b - 5$ B、若 $a = b$ ，则 $2 a = 3 b$ C、若 $a + b = 2 b$ ，则 $a = b$ D、若 $a = b + 2$ ，则 $2 a = 2 b + 2$

查看试题解析
6. 直棱柱的侧面都是（）

A、正方形 B、长方形 C、五边形 D、以上都不对

查看试题解析
7. 已知a²+2a=1，则代数式2a²+4a﹣1的值为（）．

A、0 B、1 C、﹣1 D、﹣2

查看试题解析
8. 下列说法中，正确的是（　　）

A、两条射线组成的图形叫做角 B、有公共端点的两条线段组成的图形叫做角 C、角可以看做是由一条射线绕着它的端点旋转而形成的图形 D、角可以看做是由一条线段绕着它的端点旋转而形成的图形

查看试题解析
9. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）

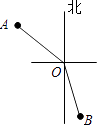A、69° B、111° C、141° D、159°

查看试题解析
10. 某校为开展第二课堂，组织调查了本校150名学生各自最喜爱的一项体育活动，制成了如下扇形统计图，则在该被调查的学生中，跑步和打羽毛球的学生人数分别是（）

A、30，40 B、45，60 C、30，60 D、45，40

查看试题解析
11. 如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（）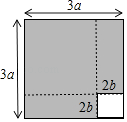

A、3a+2b B、3a+4b C、6a+2b D、6a+4b

查看试题解析
12. 如图所示，将一张长方形纸片斜折过去，使顶点A落在 $A^{'}$ 处，BC为折痕，然后再把BE折过去，使之与B $A^{'}$ 重合，折痕为BD，若∠ABC＝58°，则求∠ $E^{'}$ BD的度数（）

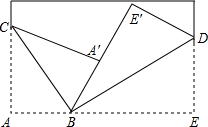A、29° B、32° C、58° D、64°

查看试题解析

二、填空题

13. 比较大小： $- (- \frac{2}{7})$ $- \frac{3}{8}$ ．

查看试题解析
14. 在数轴上到表示-2的点距离为5的点所表示的有理数是 .

查看试题解析
15. 一个角的余角比它的补角的 $\frac{1}{3}$ 多12°，则这个角为.

查看试题解析
16. 若 $a + 9 = b + 8 = c + 7$ ，则 $(a - b)^{2} + (b - c)^{2} - (c - a)^{2} =$ .

查看试题解析
17. 已知代数式 $3 x^{2} - 4 x - 6$ 的值是9，则代数式 $x^{2} - \frac{4}{3} x + 2$ 的值是.

查看试题解析
18. 为提高服务质量，学校食堂对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序：①绘制扇形统计图；②收集最受学生欢迎菜品的数据；③利用扇形统计图分析出最受学生欢迎的菜品；④整理所收集的数据.请按正确的调查统计顺序重新排序（只填序号）：.

查看试题解析

三、解答题

19.

(1)、计算： $- 1^{4} + 16 \div {(- 2)}^{3} \times | - 3 - 1 |$ ；

(2)、解方程： $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$ .

查看试题解析
20. 先化简，再求值： $3 (x^{2} - 2 x y) - [3 x^{2} - 2 y + 2 (x y + y)]$ ，其中 $x = - \frac{1}{2}, y = - 3$ ．

查看试题解析
21. 有理数a、b、c在数轴上的位置如图：

(1)、用“ $＞$ ”或“ $＜$ ”填空： $b - c$ 0， $a + b$ 0， $c - a$ 0.

(2)、化简： $| b - c | + | a + b | - | c - a |$ .

查看试题解析
22.
在结束了380课时初中阶段数学内容的教学后，唐老师计划安排60课时用于总复习，根据数学内容所占课时比例，绘制如下统计图表（图1～图3），请根据图表提供的信息，回答下列问题：

(1)、图1中“统计与概率”所在扇形的圆心角为度；

(2)、图2、3中的a= ， b=；

(3)、在60课时的总复习中，唐老师应安排多少课时复习“数与代数”内容？

查看试题解析
23. “中国竹乡”安吉县有着丰富的毛竹资源.某企业已收购毛竹52.5吨，根据市场信息，将毛竹直接销售，每吨可获得100元，如果对毛竹进行粗加工，每天可加工8吨，每吨可获得1000元；如果进行精加工，每天加工0.5吨，每吨可获得5000元.由于受条件限制，在同一天中只能采用一种方式加工，并且必须在一个月（30天）内将这批毛竹全部销售，为此研究了两种方案：
方案一：将毛竹全部粗加工后销售，则可获利 ▲ 元
方案二：30天时间都进行精加工，未来得及加工的毛竹，在市场上直接销售，则可获利 ▲ 元
问：是否存在第三种方案，将部分毛竹精加工，其余毛竹粗加工，并且恰好在30天内完成？若存在，求销售后所获利润；若不存在，请说明理由.

查看试题解析
24. 如图，直线AB、CD相交于点O，OA平分∠EOC.

(1)、若∠EOC=70°，求∠BOD的度数；

(2)、若∠EOC= $\frac{2}{3}$ ∠EOD，求∠BOD的度数.

查看试题解析
25. 若定义一种新的运算“*”，规定有理数a*b=4ab，如2*3=4×2×3=24．

(1)、求3*(-4)的值；

(2)、求(-2)*(6*3)的值．

查看试题解析
26. 如图，以直线AB上一点O为端点作射线OC，使∠AOC＝65°，将一个直角三角形的直角顶点放在点O处.（注：∠DOE＝90°）

(1)、如图①，若直角三角板DOE的一边OD放在射线OA上，则∠COE＝；

(2)、如图②，将直角三角板DOE绕点O顺时针方向转动到某个位置，若OC恰好平分∠AOE，求∠COD的度数；

(3)、如图③，将直角三角板DOE绕点O任意转动，如果OD始终在∠AOC的内部，试猜想∠AOD和∠COE有怎样的数量关系？并说明理由.

查看试题解析