广西壮族自治区贵港市港南区2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-02-06 类型:期末考试
一、单选题
-
1. 在数轴上与原点的距离小于8的点对应的x满足( )A、 B、或 C、 D、2. 下列各数中,是无理数的是( )A、-5 B、1.50505 C、 D、3. 下列说法中,正确的是( )A、一个数的立方根有两个,它们互为相反数 B、一个非零数的立方根与这个数同号 C、如果一个数有立方根,那么它一定有平方根 D、一个数的立方根是非负数4. 实数 的平方根为( )A、a B、±a C、± D、±5. 若关于x的不等式2﹣m﹣x>0的正整数解共有3个,则m的取值范围是( )A、﹣1≤m<0 B、﹣1<m≤0 C、﹣2≤m<﹣1 D、﹣2<m≤﹣16. 下列命题是真命题的是( )A、相等的角是对顶角 B、若实数a,b满足a2=b2 , 则a=b C、若实数a,b满足a<0,b<0,则ab<0 D、角的平分线上的点到角的两边的距离相等7. 不等式组 的解集是x>1,则m的取值范围是( )A、m≥1 B、m≤1 C、m≥0 D、m≤08. 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队预计在2012-2013赛季全部32场比赛中最少得到48分,才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是( )A、2x+(32-x)≥48 B、2x-(32-x)≥48 C、2x+(32-x)≤48 D、2x≥489. 已知表示取三个数中最小的那个数,例如:当 , , 当时,则x的值( )A、 B、 C、 D、10. 如图,在中,、的平分线 , 相交于点F, , 则( )
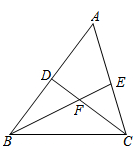 A、 B、 C、 D、11. 如图,在中,按以下步骤作图:分别以为圆心,大于的长为半径作弧,两相交于两点;②作直线交于点 , 连接.若.则的度数为( )
A、 B、 C、 D、11. 如图,在中,按以下步骤作图:分别以为圆心,大于的长为半径作弧,两相交于两点;②作直线交于点 , 连接.若.则的度数为( ) A、 B、 C、 D、12. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).
A、 B、 C、 D、12. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).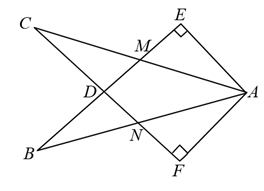 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 当有意义时,x的取值范围是.14. 比较大小:|-2|30.(选填 , , )15. 等腰三角形中, , , 则的长为 .16. 不等式的非负整数解为.17. 已知实数a、b满足 , 则的值为.18. 若关于x的方程无解,则a的值是 .
三、解答题
-
19.(1)、计算:;(2)、解方程:.20. 在中, , .
 (1)、尺规作图:求作边的垂直平分线分别交 , 于点和点﹔(保留作图痕迹,不要求写出作图过程)(2)、直接写出的形状.21. 对于任意有理数a、b、c、d,规定 , 已知 .(1)、用含x的代数式表示y;(2)、若的正整数解只有3个,求k的取值范围.22. 有理数a,b在数轴上对应点的位置如图所示.
(1)、尺规作图:求作边的垂直平分线分别交 , 于点和点﹔(保留作图痕迹,不要求写出作图过程)(2)、直接写出的形状.21. 对于任意有理数a、b、c、d,规定 , 已知 .(1)、用含x的代数式表示y;(2)、若的正整数解只有3个,求k的取值范围.22. 有理数a,b在数轴上对应点的位置如图所示. (1)、结合数轴可知:(用“>、=或<”填空);(2)、结合数轴化简.23. 为全力保障人民群众身体健康和生命安全,我区开展新一轮全员核酸检测.第一天甲、乙两支核酸检测队共32人在某乡镇进行核酸采样,当天采样13840人.已知甲检测队平均每人每天采样420人,乙检测队平均每人每天采样440人.(1)、求甲、乙两支检测队各有多少人?(2)、根据计划安排,第二天需抽取甲、乙两支核酸检测队若干人共同完成对A、B、C三所学校共8640名师生的核酸采样任务,已知甲检测队抽取8人,则乙检测队需至少抽取多少人才能保证当天完成任务?24. 如图,AE平分∠BAC,∠CAE=∠CEA.
(1)、结合数轴可知:(用“>、=或<”填空);(2)、结合数轴化简.23. 为全力保障人民群众身体健康和生命安全,我区开展新一轮全员核酸检测.第一天甲、乙两支核酸检测队共32人在某乡镇进行核酸采样,当天采样13840人.已知甲检测队平均每人每天采样420人,乙检测队平均每人每天采样440人.(1)、求甲、乙两支检测队各有多少人?(2)、根据计划安排,第二天需抽取甲、乙两支核酸检测队若干人共同完成对A、B、C三所学校共8640名师生的核酸采样任务,已知甲检测队抽取8人,则乙检测队需至少抽取多少人才能保证当天完成任务?24. 如图,AE平分∠BAC,∠CAE=∠CEA.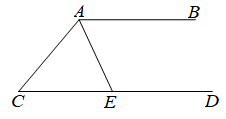 (1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.
(1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.
