沪科版2022~2023学年七年级上学期期末考试数学预测卷（二）

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列说法：①整数和分数统称为有理数；②绝对值是它本身的数只有0；③两数之和一定大于每个加数；④如果两个数积为0，那么至少有一个因数为0；⑤0是最小的有理数，其中正确的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列说法中正确的是（）

A、 $\frac{1}{2}$ πx³的系数是 $\frac{1}{2}$ B、y﹣x²y+5xy²的次数是7 C、4不是单项式 D、﹣2xy与4yx是同类项

查看试题解析
3. 2022年北京冬奥会计划于2月4日开幕.作为2022年北京冬奥会雪上项目的主要举办地，张家口市崇礼区建成7家大型滑雪场，拥有169条雪道，共162000米.数字162000用科学记数法表示为（）

A、 $162 \times 1 0^{3}$ B、 $16.2 \times 1 0^{4}$ C、 $1.62 \times 1 0^{5}$ D、 $0.162 \times 1 0^{6}$

查看试题解析
4. 为了解曲靖市某区七年级3000名学生的视力情况，从中抽查200名学生的视力进行统计分析，下列四个判断正确的是（）

A、3000名学生是总体 B、样本容量是200名 C、每名学生是总体的一个样本 D、200名学生的视力是样本

查看试题解析
5. 甲､乙两车分别从A､B两地同时出发，相向而行，若快车甲的速度为 $60 k m / h$ ，慢车乙的速度比快车甲慢 $4 k m / h$ ， A､B两地相距 $80 k m$ ，求两车从出发到相遇所行时间，如果设 $x h$ 后两车相遇，则根据题意列出方程为（）

A、 $\frac{x}{80} + \frac{x - 4}{80} = 60$ B、 $x (x - 4) = 80$ C、 $60 x + (60 - 4) x = 80$ D、 $60 x + 60 (x - 4) = 80$

查看试题解析
6. 点 $O$ 在直线 $A B$ 上，射线 $O C$ 、 $O D$ 在直线 $A B$ 的同侧，若 $∠ A O D = 148.9 °$ ， $∠ B O C = 54 ° 30^{'}$ ，则 $∠ C O D$ 的度数为（）

A、 $23 ° 30^{'}$ B、 $23 ° 24^{'}$ C、 $22 ° 30^{'}$ D、 $22 ° 24^{'}$

查看试题解析
7. “双十一”期间，某电商决定对网上销售的某种服装按成本价提高40%后标价，又以8折（即按标价的80%）优惠卖出，结果每件服装仍可获利21元，则这种服装每件的成本是（）

A、160元 B、175元 C、170元 D、165元

查看试题解析
8.
如图，CB= $\frac{1}{2}$ AB，AC= $\frac{1}{3}$ AD，AB= $\frac{1}{3}$ AE，若CB=2cm，则AE=( )

A、6cm B、8cm C、10cm D、12cm

查看试题解析
9. 若关于x、y的方程组 ${\begin{array}{l} x + y = 2 \\ a x + 2 y = 8 \end{array}$ 的解为整数，则满足条件的所有整数a的值的和为（）

A、6 B、9 C、12 D、16

查看试题解析
10. 如图所示的是中国南宋数学家杨辉在详解《九章算法》中出现的三角形状的数列，又称为“杨辉三角形”该三角形中的数据排列有着一定的规律，若将其中 $-$ 组斜数列用字母 $a_{1}$ 、 $a_{2}$ ， $a_{3}$ ， $\dots$ 代替，如图 $2$ ，则 $a_{99} + a_{100}$ 的值为（）

A、9801 B、10000 C、10201 D、10500

查看试题解析

二、填空题（每题5分，共25分）

11. 比较两个数的大小：﹣ $\frac{7}{6}$ ﹣ $\frac{8}{7}$

查看试题解析
12. 计算： $12 ° 25^{'} 10 ″ \times 3 + 18 ° 12^{'} 45 ″ =$ ．

查看试题解析
13. 已知 $6 a^{m} b^{3}$ 与 $- \frac{3}{7} a^{3} b^{n + 1}$ 是同类项，则 $m - n$ = ．

查看试题解析
14. 若方程 $2 x - 1 = 3$ 的解与方程 $\frac{x - m}{2} = 2$ 的解相同，则 $m =$ ．

查看试题解析
15. 定义一种树对正整数n的“F”运算：①当n的奇数时F（n）=3n+1；②当n为偶数时，F（n）= $\frac{n}{2^{k}}$ （其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24则：

若n=13，则第2019次“F”运算的结果是

查看试题解析

三、计算题（共3题，共18分）

16. 计算：（﹣3）³÷2 $\frac{1}{4} \times {(- \frac{2}{3})}^{2} + 4 - 2 \times (- \frac{1}{3})$ .

查看试题解析
17. 解方程： $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$

查看试题解析
18. 先化简，再求值： $8 a^{2} b + 2 (2 a^{2} b - 3 a b^{2}) - 3 (4 b^{2} b - a b^{2})$ ，其中 $| a + 1 | + {(b - 1)}^{2} = 0$ ．

查看试题解析

四、综合题（共6题，共67分）

19. 某中学为了丰富学生校园生活，满足学生的多元文化需求，促进学生身心健康和谐发展，学校开展了丰富多彩的社团活动，该校开展的社团活动有5个类别，他们分别是A：动漫社团，B：轮滑社团，C：音乐社团，D：诗歌社团，E：书法社团，每个学生必须参加且只能参加一个类别的社团活动.该校七年级某同学在学习完“数据的收集、整理与描述”知识后，想通过所学知识分析全校500名同学参加社团活动的情况，于是他在该校随机抽取40名同学开展了一次调查统计分析，过程如下：
收集数据：记录40名同学参加社团活动的类别情况如下：

整理数据：列统计表、绘扇形图如下：

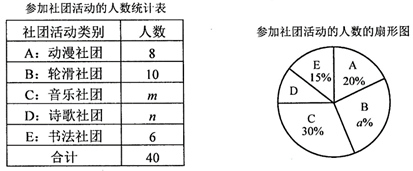
请根据上面的调查统计分析的过程和结果，解答下列问题；

(1)、写出m、n、a的值；

(2)、求社团“D：诗歌社团”所在的扇形图的圆心角的度数；

(3)、估计全校参加“D：诗歌社团”和“E：书法社团”的人数.

查看试题解析
20. 观察下列算式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，….

(1)、通过观察以上算式，猜想开写出 $\frac{1}{n (n + 1)} =$ （ $n$ 为正整数）.

(2)、直接写出下列算式的结果：
$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \cdot \cdot \cdot + \frac{1}{2019 \times 2020} + \frac{1}{2020 \times 2021} =$ .

查看试题解析
21.

(1)、如图，点 $C$ ， $D$ 在线段 $A B$ 上，点 $D$ 为线段BC的中点，若 $A C = 3 cm$ ， $B D = 8 cm$ ，求线段 $A B$ 的长.

(2)、如图，已知 $∠ C O B = 4 ∠ A O C$ ， $O D$ 平分 $∠ A O B$ ，且 $∠ C O D = 30^{\circ}$ ，求 $∠ A O B$ 的度数.

查看试题解析
22. 点O为直线AB上一点，过点O作射线OC ，使∠BOC=65°，将一直角三角板的直角顶点放在点O处.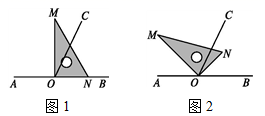

(1)、如图1，将三角板MON的一边ON与射线OB重合时，则∠MOC=

(2)、如图2，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的平分线，求∠BON和∠CON的度数．

查看试题解析

23. 十一期间，各大商场掀起购物狂潮，现有甲、乙、丙三个商场开展的促销活动如表所示：

商场	优惠活动
甲	全场按标价的6折销售
乙	实行“满100元送100元的购物券”的优惠，购物券可以在再购买时冲抵现金（如：顾客购衣服220元，赠券200元，再购买裤子时可冲抵现金，不再送券）
丙	实行“满100元减50元的优惠”（比如：某顾客购物220元，他只需付款120元）

根据以上活动信息，解决以下问题：

(1)、三个商场同时出售一件标价290元的上衣和一条标价270元的裤子，王阿姨想买这一套衣服，她应该选择哪家商场？

(2)、黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子，最后付款额也一样，请问这条裤子的标价是多少元？

查看试题解析

24. 已知数轴上两点 $A$ ， $B$ 对应的数分别为 $- 8$ 和4，点 $P$ 为数轴上一动点，若规定：点 $P$ 到 $A$ 的距离是点 $P$ 到 $B$ 的距离的3倍时，我们就称点 $P$ 是关于 $A \to B$ 的“好点”.

(1)、若点 $P$ 到点 $A$ 的距离等于点 $P$ 到点 $B$ 的距离时，求点 $P$ 表示的数是多少；

(2)、①若点 $P$ 运动到原点 $O$ 时，此时点 $P$ ▲ 关于 $A \to B$ 的“好点”（填是或者不是）；
②若点 $P$ 以每秒1个单位的速度从原点 $O$ 开始向右运动，当点 $P$ 是关于 $A \to B$ 的“好点”时，求点 $P$ 的运动时间；

(3)、若点 $P$ 在原点的左边（即点 $P$ 对应的数为负数），且点 $P$ ， $A$ ， $B$ 中，其中有一个点是关于其它任意两个点的“好点”，请直接写出所有符合条件的点 $P$ 表示的数.

查看试题解析