沪科版2022~2023学年七年级上学期期末考试数学预测卷（一）

试卷更新日期：2023-02-06 类型：期末考试

进入出卷网下载

一、单选题（每题4分，共40分）

1. $| - \frac{1}{2022} |$ 的倒数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、-2022 D、2022

查看试题解析
2. 下列计算中正确的是（）

A、a²+a³＝a⁵ B、|﹣a²|＝﹣a² C、（﹣a）³＝a³ D、（﹣a²）＝﹣a²

查看试题解析
3. “多少事，从来急；天地转，光阴迫.一万年太久，只争朝夕.”伟人毛泽东通过这首《满江红·和郭沫若同志》告诉我们青年学生：要珍惜每分每秒，努力工作，努力学习.一天时间为86400秒，用科学记数法表示这一数字是（）

A、 $864 \times 1 0^{2}$ B、 $8.64 \times 1 0^{5}$ C、 $8.64 \times 1 0^{4}$ D、 $0.864 \times 1 0^{5}$

查看试题解析
4. 某校有3000名学生在线观看了“天宫课堂”第二课，并参加了关于“你最喜爱的太空实验”的问卷调查，从中抽取500名学生的调查情况进行统计分析，以下说法错误的是（）

A、3000名学生的问卷调查情况是总体 B、500名学生的问卷调查情况是样本 C、500名学生是样本容量 D、每一名学生的问卷调查情况是个体

查看试题解析
5. 某车间原计划用15小时生产一批零件，实际每小时多生产了10件，用了13小时不但完成了任务，而且还多生产了80件，设原计划每小时生产 $x$ 个零件，那么下列方程正确的是（）

A、 $\frac{1}{15} x = \frac{1}{13} (x + 10) + 80$ B、 $\frac{1}{15} (x + 10) = \frac{1}{13} x + 80$ C、 $15 x = 13 (x + 10) + 80$ D、 $13 (x + 10) = 15 x + 80$

查看试题解析
6. 下列说法中正确的是（）

A、射线 $AB$ 和射线 $B . A$ 是同一条射线 B、延长线段 $AB$ 和延长线段 $BA$ 的含义是相同的 C、若 $A$ ， $B$ ， $C$ 三点在同一直线上，且 $AB = 2 CB$ ，则点 $C$ 是线段 $AB$ 的中点 D、若 $∠ A = 21 ° 18'$ ， $∠ B = 21 ° 28 ″$ ， $∠ C = 21.25 °$ ，则有 $∠ A > ∠ C > ∠ B$

查看试题解析
7. 商店元旦促销，某款衣服打8折销售．每件比标价少35元，仍获利15元．下列说法：①衣服标价为每件175元；②衣服促销单价为140元；③衣服的进价为每件125元；④不打折时商店的利润为每件50元．正确的共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 如图，点A，B在线段EF上，点M，N分别是线段EA，BF的中点，EA：AB：BF＝1：2：3，若MN＝8cm，则线段EF的长为（）cm

A、10 B、11 C、12 D、13

查看试题解析
9. 如图． $∠ A O B = a$ ， $O A_{1}$ 、 $O B_{1}$ 分别是∠AOM和∠MOB的平分线， $O A_{2}$ 、 $O B_{2}$ 分别是 $∠ A_{1} O M$ 和 $∠ M O B_{1}$ 的平分线， $O A_{3}$ 、 $O B_{3}$ 分别是 $∠ A_{2} O M$ 和 $∠ M O B_{2}$ 的平分线，…， $O A_{n}$ 、分别是 $∠ A_{n - 1} O M$ 和 $∠ M O B_{n - 1}$ 的平分线，则 $∠ A_{n} O B_{n}$ 的度数是（）

A、 $\frac{a}{n}$ B、 $\frac{a}{2^{n - 1}}$ C、 $\frac{a}{2^{n}}$ D、 $\frac{a}{n^{2}}$

查看试题解析
10. 用如图 $①$ 中的长方形和正方形纸板作侧面和底面，做成如图 $②$ 的竖式和横式的两种无盖纸盒.现有 $m$ 张正方形纸板和 $n$ 张长方形纸板，如果做两种纸盒若干个，恰好将纸板用完，则 $m + n$ 的值可能是（）

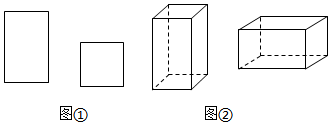A、2019 B、2020 C、2021 D、2022

查看试题解析

二、填空题（每题5分，共25分）

11. 比较大小： $- 1.5$ $- 1 \frac{1}{5}$ （填“ $>$ ”或“ $=$ ”或“ $<$ ”）．

查看试题解析
12. 若 $- 2 a^{m} b^{4}$ 与 $5 a^{3} b^{2 + n}$ 是同类项，则 $- m + n$ 的值是．

查看试题解析
13. 如图，按照程序图计算，当输入正整数 $x$ 时，输出的结果是 $161$ ，则输入的 $x$ 的值可能是．

查看试题解析
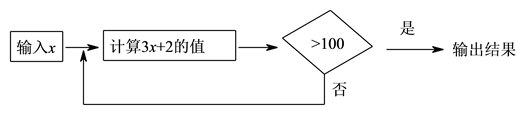14. 若 $a$ 、 $b$ 为定值，关于 $x$ 的一次方程 $\frac{2 k x + a}{3} - \frac{x - b k}{6} = 2$ 无论 $k$ 为何值时，它的解总是 $x = 1$ ，则 $(2 a + 3 b)^{2022}$ 的值为．

查看试题解析
15. 如图，把一长方形纸片ABCD的一角沿AE折叠，点D的对应点 $D ′$ 落在∠BAC内部．若 $∠ C A E = 2 ∠ B A D^{'}$ ，且 $∠ C 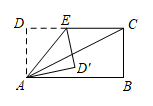A D^{'} = 15 °$ ，则∠DAE的度数为．

查看试题解析

三、计算题（共3题，共18分）

16. 计算：

(1)、 $20 - (- 15) + 8 + (- 17)$

(2)、 $- 1^{4} - (- 5 \frac{1}{2}) \times \frac{6}{11} + {(- 2)}^{3} \div | - 3^{2} + 1 |$

查看试题解析
17. 解方程： $x - \frac{x - 1}{2} = 2 - \frac{x + 2}{5}$

查看试题解析
18. 先化简，再求值： $(2 a^{2} - 3 a + 1) + 3 (a - 2 a^{2} - \frac{1}{3})$ ，其中 $a = - 1$ ．

查看试题解析

四、综合题（共6题，共67分）

19. 某中学开设了书法、绘画、乐团、合唱等艺术类社团，全校每名学生选择了其中一项活动，为了解学生的报名情况，张老师抽选了一部分学生进行调查，并绘制了两个不完整的统计图，请你依据统计图中的信息，回答下列问题：

(1)、本次抽样调查共抽取了名学生；通过计算补全条形统计图；

(2)、求图2中表示合唱的扇形圆心角的度数；

(3)、若全校共有1600名学生，请你估计全校选择参加乐团的学生有多少名？

查看试题解析
20. 观察下列等式并回答问题．
第1个等式： $a_{1} = \frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ．
第2个等式： $a_{2} = \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ．
第3个等式： $a_{3} = \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ．
……

(1)、则第4个等式为，第n个等式为．

(2)、求 $a_{1} + a_{2} + a_{3} + a_{4} + \dots + a_{2023}$ 的值．

查看试题解析
21. 如图，线段 $A C$ 上依次有 $D 、 B 、 E$ 三点， $A D = \frac{1}{2} D B$ ， $E$ 是 $B C$ 的中点， $B E = \frac{1}{5} A C = 2$ ．

(1)、求线段 $A B$ 的长；

(2)、求线段 $D E$ 的长．

查看试题解析
22. 已知OD、OE分别是∠AOB、∠AOC的角平分线．

(1)、如图1，OC是∠AOB外部的一条射线．
①若∠AOC＝32°，∠BOC＝126°，则∠DOE＝ ▲ °；
②若∠BOC＝164°，求∠DOE的度数；

(2)、如图2，OC是∠AOB内部的一条射线，∠BOC＝n°，用n的代数式表示∠DOE的度数．

查看试题解析
23. 某社区超市第一次用6000元购进甲、乙两种商品，其中甲商品的件数比乙商品件数的2倍少30件，甲、乙两种商品的进价和售价如表：

甲
乙
进价（元/件）
22
30
售价（元/件）
29
40

(1)、该超市购进甲、乙两种商品各多少件？

(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(3)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品销售一部分后出现滞销，于是超市决定将剩余的乙商品五折促销，若在本次销售过程中超市共获利2350元，则以五折售出的乙商品有多少件？

查看试题解析
24. 已知 $b$ 是最小的正整数， $a$ ， $b$ 满足 ${(c - 5)}^{2} + | a + b | = 0$ ，且 $a$ ， $b$ ， $c$ 分别对应数轴上的点 $A$ ， $B$ ， $C$ ．

(1)、请直接写出 $a$ ， $b$ ， $c$ 的值： $a =$ ， $b =$ ， $c =$ ．

(2)、若点 $P$ 为一动点，从点 $A$ 出发以每秒2个单位长度的速度向右运动，则点 $P$ 运动几秒后，点 $P$ 到点 $A$ 的距离是点 $P$ 到点 $C$ 的距离的2倍？

(3)、点 $A$ 以每秒1个单位长度的速度向左运动，同时点 $B$ 和点 $C$ 分别以每秒2个单位长度和5个单位长度的速度向右运动．点 $B$ 与点 $C$ 之间的距离表示为 $B C$ ，点 $A$ 与点 $B$ 之间的距离表示为 $A B .$ 假设运动时间为 $t s$ ， $B C - A B$ 的值是否随着时间 $t$ 的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析

	甲	乙
进价（元/件）	22	30
售价（元/件）	29	40