2023年浙教版数学八年级下册3.2中位数与众数同步测试

试卷更新日期：2023-02-03 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. “杂交水稻之父”袁隆平培育的超级杂交水稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势，从稻田中随机抽取7株水稻苗，测得苗高（单位： $cm$ ）分别是：23，24，23，25，26，23，25.则这组数据的众数和中位数分别是（）

A、24，25 B、23，23 C、23，24 D、24，24

查看试题解析
2. 淄川区域内的风景文化名胜很多．其中蒲松龄故居、服装城、 $1954$ 文化广场、潭溪山、马鞍山抗日遗址都有很好的风光和丰富的文化底蕴，某班同学分小组到以上五个地方进行研学旅行，人数分别为 $12 ， 5 ， 11 ， 5 ， 7$ ，这组数据的众数和中位数分别是（）

A、5人，7人 B、5人，11人 C、5人，12人 D、7人，11人

查看试题解析
3. 为了了解班级同学的家庭用水情况，小明在全班50名同学中，随机调查了10名同学家庭中一年的月平均用水量（单位：吨），绘制了条形统计图如图所示．这10名同学家庭中一年的月平均用水量的中位数是（）

A、7.5 B、7 C、6.5 D、6

查看试题解析
4. 欣欣商店在一段时间内销售了四种饮料共100瓶，各品牌饮料的销售量如表，根据表中数据，建议该商店进货数量最多的品牌是（）

品牌

甲

乙

丙

丁

销售量（瓶）

15

30

12

43

A、甲品牌 B、乙品牌 C、丙品牌 D、丁品牌

查看试题解析
5. 若一组数据 $x ， 1 ， 4$ 的中位数为3，则 $x$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 当五个整数从小到大排列，中位数为8，若这组数中的唯一众数为10，则这5个整数的和最大可能是（）

A、39 B、40 C、41 D、42

查看试题解析
7. 学校为了解学生的睡眠情况，随机调查50名学生的睡眠时间，数据如下表所示：则50名学生睡眠时间的众数，中位数分别是（）
时间（小时）
6
7
8
9
10
人数
4
16
19
8
3

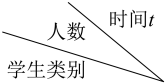
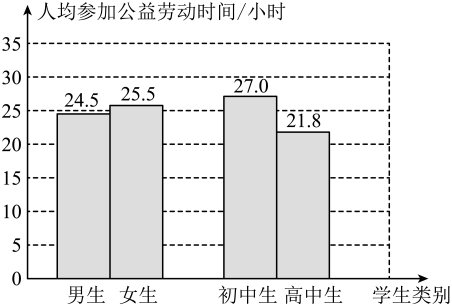
A、8，8 B、19，8 C、19，75 D、8，7.5

查看试题解析
8. 为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛，对甲、乙两人进行了5次投篮试投比赛，试投每人每次投球10个，两人5次试投的成绩统计图如图所示．以下说法错误的是（）

A、甲同学5次试投进球个数的众数是8 B、甲、乙两名同学投篮成绩甲较稳定 C、甲、乙同学5次试投进球个数的平均数相同 D、乙同学5次试投进球个数的中位数是8

查看试题解析
9. 由小到大排列一组数据a₁、a₂、a₃、a₄、a₅ ，其中每个数据都小于0，则对于样本a₁、a₂、－a₃、－a₄、－a₅、0的中位数可表示为（）

A、 $\frac{a_{2} - a_{3}}{2}$ B、 $\frac{a_{2} - a_{5}}{2}$ C、 $\frac{0 - a_{5}}{2}$ D、 $\frac{0 - a_{3}}{2}$

查看试题解析
10. 某校共有200名学生．为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据．下图是根据数据绘制的统计图表的一部分．下面有四个推断：
①这200名学生参加公益劳动时间的平均数一定在 $24.5 \sim 25.5$ 之间；②这200名学生参加公益劳动时间的中位数在 $20 ∼ 30$ 之间；③这200名学生中的初中生参加公益劳动时间的中位数一定在 $20 ∼ 30$ 之间；④这200名学生中的高中生参加公益劳动时间的中位数可能在 $20 ∼ 30$ 之间．
所有合理推断的序号是（）
$0 \leq t < 10$
$10 \leq t < 20$
$20 \leq t < 30$
$30 \leq t < 40$
$t \geq 40$
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中

A、①③ B、②④ C、①②③ D、①②③④

查看试题解析

二、填空题（每题4分，共24分）

11. 某品牌专卖店9月份销售了20双运动鞋，其尺码和数量统计如下表：
尺码
38
39
40
41
42
数量
2
4
5
6
3
这20双运动鞋尺码的众数是．

查看试题解析
12. 已知一组数据为1，10，6，4，7，4，则这组数据的众数为．

查看试题解析
13. 小燕的父亲近六个月的手机话费（单位：元）如下：81，75，70，64，98，92．这组数据的中位数是．

查看试题解析
14. 已知4个正数a₁ ， a₂ ， a₃ ， a₄的平均数是a，且a₁＞a₂＞a₃＞a₄ ，则数据a₁ ， a₂ ， 0，a₃ ， a₄的平均数和中位数分别是，．

查看试题解析
15. 一组数据18，22，15，13，x，7，它的中位数是16，则x的值是．

查看试题解析
16. 南吕是国家历史文化名城，其名源于“昌大南疆，南方昌盛”之意，市内的滕王阁、八一起义纪念馆、海昏候遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴．某班同学分小组到以上五个地方进行研学，人数分别为：12，5，11，5，7（单位：人），这组数据的中位数是．

查看试题解析

三、解答题（共8题，共66分）

17. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
分别计算这些运动员成绩的平均数、中位数、众数（结果保留小数点后两位）．

查看试题解析
18. 某校男子足球队的年龄分布如上面的条形图所示，请找出这些队员年龄的平均数、众数、中位数，并解释它们的意义．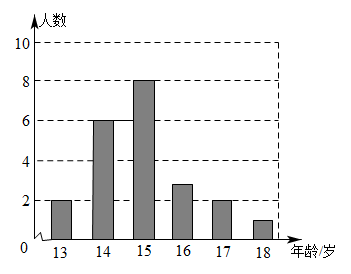

查看试题解析
19. 为讴歌抗击新冠肺炎的白衣战士，某校七年级举行了“新时代最可爱的人”主题演讲比赛 $.$ 七年级甲，乙两班分别选5名同学参加比赛 $.$ 如图是根据其预赛成绩绘制的折线统计图，请你根据统计图提供的信息完成以下问题：

(1)、求甲班成绩的中位数和乙班成绩的众数；

(2)、学校决定在甲，乙两班中选取预赛成绩较好的5人参加该活动的区级比赛，求这5人预赛成绩的平均数．

查看试题解析

20. 某中学九年级组织了一次数学计算比赛（禁用计算器），每班选25名同学参加比赛，成绩分为

A

，

B

，

C

，

D

四个等级，其中

A

等级得分为100分，

B

等级得分为85分，

C

等级得分为75分，

D

等级得分为60分，数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图，请根据提供的信息解答下列问题．

(1)、把一班竞赛成绩统计图补充完整．

(2)、求出下表中

a

，

b

，

c

的值；

	平均数（分）	中位数（分）	众数（分）
一班	$a$	$b$	85
二班	84	75	$C$

(3)、请从以下给出的两个方面对这次比赛成绩的结果进行分析：①从平均数、众数方面来比较一班和二班的成绩；②从

B

级以上（包括

B

级）的人数方面来比较一班和二班的成绩．

查看试题解析

21. 某次数学测试，圆圆同学所在的学习小组其他同学的平均分为75分，圆圆说，“我的分是100分，我们学习小组的平均分恰好是80分”．

(1)、圆圆同学所在的学习小组有多少人？

(2)、已知该学习小组本次测试得分的众数是90分，最低分为50分，求该学习小组本次测试得分的中位数．

查看试题解析

22. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试．现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：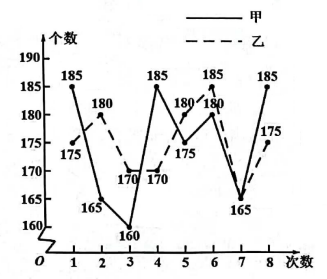

	平均数	中位数	众数
甲	175	b	c
乙	a	175	180，175，170

(1)、求a， b，c的值.

(2)、根据以上的数据分析，请你运用所学统计知识，评价甲乙两名男生一分钟跳绳成绩谁优.

查看试题解析

23. 某校组织了一次环保知识竞赛，九年级每班选25名同学参加比赛，成绩分为

A

，

B

，

C

，

D

四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将901班和902班同学的成绩进行整理并绘制成如图的统计图表.请根据信息解答下列问题：

(1)、把901班竞赛成绩统计图补充完整；

(2)、求出统计表中

a

，

b

，

c

的值；

(3)、请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析：

$①$ 从平均数和中位数方面来比较901班和902班的成绩；

$②$ 从平均数和众数方面来比较901班和902班的成绩；

$③$ 从 $B$ 级以上（包括 $B$ 级）的人数方面来比较901班和902班的成绩.

班级	平均数（分）	中位数（分）	众数（分）
901	$a$	$b$	90
902	87.6	80	$c$

查看试题解析

24. 为落实国家对学生体质健康的基本要求，促进学生积极参加体育锻炼，提高体质健康水平，某校在开学初对九年级500名学生进行了第一次体质测试（满分50分），整理得如下不完整的统计表.之后制定体育锻炼计划，每天按计划进行锻炼，期中时再进行第二次体质测试，整理后绘制得如下不完整的扇形统计图（测试得分的分组与第一次相同）.

九年级学生第一次体质测试得分的频数分布表

组别	体质测试得分（分）	组中值	频数（人）
A	$0 \leq x \leq 10$	5	15
B	$10 < x \leq 20$	15	50
C	$20 < x \leq 30$	25	100
D	$30 < x \leq 40$	35	a
E	$40 < x \leq 50$	45	130

(1)、频数分布表中a的值为，扇形统计图中C部分所对应的圆心角的度数为；

(2)、请选择一个合适的统计量，评价该校九年级学生这半学期每天按计划进行体育锻炼的效果；

(3)、若体质测试得分达到30分以上为达标，则九年级学生第二次体质测试达标率比第一次提升了多少？

查看试题解析

		$0 \leq t < 10$	$10 \leq t < 20$	$20 \leq t < 30$	$30 \leq t < 40$	$t \geq 40$
性别	男	7	31	25	30	4
性别	女	8	29	26	32	8
学段	初中		25	36	44	11
学段	高中

品牌	甲	乙	丙	丁
销售量（瓶）	15	30	12	43

时间（小时）	6	7	8	9	10
人数	4	16	19	8	3

尺码	38	39	40	41	42
数量	2	4	5	6	3

成绩/m	1.50	1.60	1.65	1.70	1.75	1.80
人数	2	3	2	3	4	1

2023年浙教版数学八年级下册3.2中位数与众数 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学八年级下册3.2中位数与众数同步测试