2023年上海市中考模拟试卷(1)
试卷更新日期:2023-02-03 类型:中考模拟
一、单选题(每题4分,共24分)
-
1. 在实数 , , , , , , , 0.1010010001中,无理数有( )A、2个 B、3个 C、4个 D、5个2. 关于x的分式方程+3=无解,m的值为( )A、7 B、-7 C、1 D、-13. 如图,点B在y轴的正半轴上,点C在反比例函数的图象上,菱形的面积为8,则k的值为( )
 A、-4 B、4 C、-2 D、24. 一组数据为7,9,9,11,若添加一个数据9,则发生变化的统计量是( )A、方差 B、众数 C、中位数 D、平均数5. 已知四边形 中, ,下列判断中的正确的是( )A、如果 ,那么四边形 是等腰梯形 B、如果 ,那么四边形 是菱形 C、如果AC平分BD,那么四边形 是矩形 D、如果 ,那么四边形 是正方形6. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )
A、-4 B、4 C、-2 D、24. 一组数据为7,9,9,11,若添加一个数据9,则发生变化的统计量是( )A、方差 B、众数 C、中位数 D、平均数5. 已知四边形 中, ,下列判断中的正确的是( )A、如果 ,那么四边形 是等腰梯形 B、如果 ,那么四边形 是菱形 C、如果AC平分BD,那么四边形 是矩形 D、如果 ,那么四边形 是正方形6. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )①△BDE∽△DPE;②;③;④tan∠DBE=.
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(每题4分,共48分)
-
7. 计算.8. 函数 , 则 .9. 已知 , 是一次函数的图象上的两个点,则 , 的大小关系是 .10. 若是关于的一元二次方程的一个根,则的值为.11. 某一天,小林与小李都要去核酸检测点进行核酸检测,若当地共有A,B,C,D四个核酸检测点,则在随机选择的情况下,两人都在同一检测点进行检测的概率是.12. 若将抛物线y=x2-6x+5所在的平面直角坐标系中的x轴向上平移1个单位,把y轴向右平移2个单位,则该抛物线在新的平面直角坐标系下的函数表达式为 .13. 为了估计鱼塘中的鱼数,养鱼者首先从鱼塘中打捞100条鱼,在每一条鱼身上做好记号后把这些鱼放归鱼塘,再从鱼塘中打捞10条鱼,如果在这10条鱼中有2条鱼是有记号的,那么估计鱼塘中鱼的条数为条.14. 如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
 15. 如图,在△ABC中,点D在边AB上,且= , 点E是AC的中点,= , = , 试用向量 , 表示向量 , 那么= .
15. 如图,在△ABC中,点D在边AB上,且= , 点E是AC的中点,= , = , 试用向量 , 表示向量 , 那么= .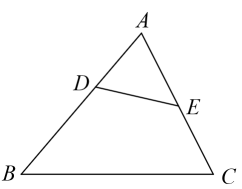 16. 甲、乙两位同学骑自行车,从各自家出发上学,他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示,则乙比甲早到分钟.
16. 甲、乙两位同学骑自行车,从各自家出发上学,他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示,则乙比甲早到分钟.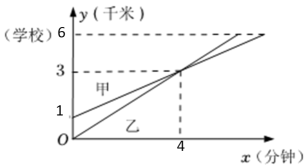 17. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是.
17. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是. 18. 矩形 中, =5, =12,如果分别以 , 为圆心的两圆相切,点 在⊙ 内,点 在⊙ 外,那么⊙ 的半径 的取值范围是 .
18. 矩形 中, =5, =12,如果分别以 , 为圆心的两圆相切,点 在⊙ 内,点 在⊙ 外,那么⊙ 的半径 的取值范围是 .三、解答题(共7题,共78分)
-
19. 有理数 在数轴上的位置如图所示:化简:
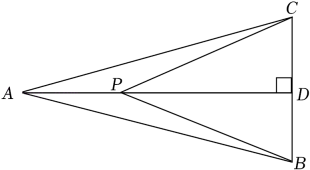
 20. 解不等式组: , 并利用数轴表示不等式组的解集.21. 如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m, CD=20m。AB和CD之闻有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上。求两幢建筑物之间的距离BD.(结果精确到0.1m)[参考数据: sin42°=0.67,cos42°=0.74,tan42°=0。90]
20. 解不等式组: , 并利用数轴表示不等式组的解集.21. 如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m, CD=20m。AB和CD之闻有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上。求两幢建筑物之间的距离BD.(结果精确到0.1m)[参考数据: sin42°=0.67,cos42°=0.74,tan42°=0。90] 22. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其他两位成员交流的情况.
22. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其他两位成员交流的情况.小张:“该商品的进价为24元/件.”
成员甲:“当定价为40元/件时,每天可售出480件.”
成员乙:“若单价每涨1元,则每天少售出20件;若单价每降1元,则每天多售出40件.”根据他们的对话,请你求出要使该商品每天获利7680元,应该怎样合理定价?
23. 如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)、如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
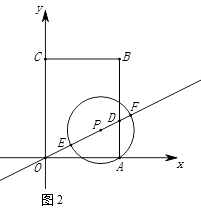
24. 如图,点 , 分别在 轴和 轴的正半轴上, , 的长分别为 的两个根 ,点 在 轴的负半轴上,且 ,连接 . (1)、求过 , , 三点的抛物线的函数解析式;(2)、点 从点 出发,以每秒2个单位长度的速度沿 运动到点 ,点 从点 出发,以每秒1个单位长度的速度沿 运动到点 ,连接 ,当点 到达点 时,点 停止运动,求 的最大值;(3)、 是抛物线上一点,是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.25. 如图1,直角坐标系中有一矩形OABC , 其中 O是坐标原点,点A , C分别在x轴和y轴上,点B的坐标为(3,4),直线 交AB于点D , 点P是直线 位于第一象限上的一点,连接PA , 以PA为半径作⊙P ,
(1)、求过 , , 三点的抛物线的函数解析式;(2)、点 从点 出发,以每秒2个单位长度的速度沿 运动到点 ,点 从点 出发,以每秒1个单位长度的速度沿 运动到点 ,连接 ,当点 到达点 时,点 停止运动,求 的最大值;(3)、 是抛物线上一点,是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.25. 如图1,直角坐标系中有一矩形OABC , 其中 O是坐标原点,点A , C分别在x轴和y轴上,点B的坐标为(3,4),直线 交AB于点D , 点P是直线 位于第一象限上的一点,连接PA , 以PA为半径作⊙P ,
 (1)、连接AC , 当点P落在AC上时, 求PA的长;(2)、当⊙P经过点O时,求证:△PAD是等腰三角形;(3)、设点P的横坐标为m ,
(1)、连接AC , 当点P落在AC上时, 求PA的长;(2)、当⊙P经过点O时,求证:△PAD是等腰三角形;(3)、设点P的横坐标为m ,在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;