浙江省宁波市九校2022-2023学年高一上学期数学期末联考试卷
试卷更新日期:2023-02-03 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 下列选项中满足最小正周期为 , 且在上单调递增的函数为( )A、 B、 C、 D、3. “”是“函数在上单调递增”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知幂函数(且)过点 , 则函数的定义域为( )A、 B、 C、 D、5. 已知角的顶点与坐标原点重合,始边与轴非负半轴重合,终边经过 , 则( )A、 B、 C、 D、6. 2022年11月15日,联合国宣布,世界人口达到80亿,在过去的10年,人口的年平均增长率为1.3%,若世界人口继续按照年平均增长率为1.4%增长,则世界人口达到90亿至少需要( )年(参考数据: , , )A、8.3 B、8.5 C、8.7 D、8.97. 函数的图象最有可能的是( )A、
 B、
B、 C、
C、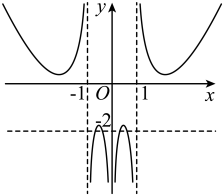 D、
D、 8. 已知 , 且 , 则的最小值为( )A、 B、1 C、 D、
8. 已知 , 且 , 则的最小值为( )A、 B、1 C、 D、二、多选题
-
9. 下列不等式错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 以下命题正确的是( )A、函数的单调递增区间为 B、函数的最小值为 C、为三角形内角,则“”是“”的充要条件 D、设是第一象限,则为第一或第三象限角11. 如图所示,角的终边与单位圆交于点 , , 轴,轴,在轴上,在角的终边上.由正弦函数、正切函数定义可知, , 的值分别等于线段 , 的长,且 , 则下列结论正确的是( )
 A、函数有3个零点 B、函数在内有2个零点 C、函数在内有1个零点 D、函数在内有1个零点;12. 已知正实数 , 满足 , 则使方程有解的实数可以为( )A、 B、2 C、 D、1
A、函数有3个零点 B、函数在内有2个零点 C、函数在内有1个零点 D、函数在内有1个零点;12. 已知正实数 , 满足 , 则使方程有解的实数可以为( )A、 B、2 C、 D、1三、填空题
-
13. 命题“ , ”的否定是 .14. 计算.15. 已知 , 则的值为.16. 设函数 , 若函数的最小值为 , 则实数的取值范围为.
四、解答题
-
17. 已知:在上恒成立;:存在使得;:存在 , 使得.(1)、若且是真命题,求实数的范围;(2)、若或是真命题,且是假命题,求实数的范围.18. 已知函数.(1)、求关于的不等式的解集;(2)、若 , 求函数在上的最小值.19. 已知函数.(1)、化简 , 并求解;(2)、已知锐角三角形内角满足 , 求的值.20. 已知函数.(1)、证明:函数在上为增函数;(2)、求使成立的的取值范围.
