四川省内江市2022-2023学年高一上学期数学期末试卷

试卷更新日期：2023-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. 设全集 $U = {0 ， 1 ， 2 ， 3 ， 4 ， 5}$ ， $A = {1 ， 2 ， 3 ， 4}$ ， $B = {1 ， 3 ， 5}$ ，则 $∁_{U} (A \cap B) =$ （）

A、 $\emptyset$ B、 ${0}$ C、 ${0 ， 2 ， 4}$ D、 ${0 ， 2 ， 4 ， 5}$

查看试题解析
2. 已知命题 $p$ ： $\forall x \in [0 ， 2]$ ， $x^{2} - 3 x + 1 > 0$ ，则命题 $p$ 的否定是（）

A、 $\exists x_{0} \in [0 ， 2]$ ， $x_{0}^{2} - 3 x_{0} + 1 \leq 0$ B、 $\exists x_{0} \in [0 ， 2]$ ， $x_{0}^{2} - 3 x_{0} + 1 < 0$ C、 $\exists x_{0} \in (- \infty ， 0) ∪ (2 ， + \infty)$ ， $x_{0}^{2} - 3 x_{0} + 1 \leq 0$ D、 $\forall x \in [0 ， 2]$ ， $x^{2} - 3 x + 1 \leq 0$

查看试题解析
3. 函数① $y = a^{x}$ ；② $y = b^{x}$ ；③ $y = c^{x}$ ；④ $y = d^{x}$ 的图象如图所示，a，b，c，d分别是下列四个数： $\frac{5}{4}$ ， $\sqrt{3}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ 中的一个，则a，b，c，d的值分别是（）

A、 $\frac{5}{4}$ ， $\sqrt{3}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ B、 $\sqrt{3}$ ， $\frac{5}{4}$ ， $\frac{1}{3}$ ， $\frac{1}{2}$ C、 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\sqrt{3}$ ， $\frac{5}{4}$ ， D、 $\frac{1}{3}$ ， $\frac{1}{2}$ ， $\frac{5}{4}$ ， $\sqrt{3}$ ，

查看试题解析
4. 函数 $f (x) = l n x - \frac{2}{x}$ 的零点所在的大致范围是（）

A、 $(\frac{1}{e} ， 1)$ B、 $(e ， + \infty)$ C、 $(1 ， 2)$ D、 $(2 ， 3)$

查看试题解析
5. 设 $a = l o g_{3} 10$ ， $b = 2^{0.3}$ ， $c = 0 . 8^{3}$ ，则（）

A、 $b < a < c$ B、 $c < a < b$ C、 $c < b < a$ D、 $a < c < b$

查看试题解析
6. 今有一组实验数据如下：

$t$

$2.0$

$3.0$

$4.0$

$5.1$

$6.18$

$v$

$1.5$

$4.02$

$7.5$

12

$18.3$

现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是（）

A、 $v = l o g_{2} t$ B、 $v = l o g_{\frac{1}{2}} t$ C、 $v = \frac{t^{2} - 1}{2}$ D、 $v = 2 t - 2$

查看试题解析
7. 已知 $f (x) = {(\frac{1}{2})}^{x^{2} - 2 a x}$ 在 $[1 ， 3]$ 上是减函数，则实数a的取值范围为（）

A、 $(- \infty ， 1]$ B、 $[1 ， 2]$ C、 $[2 ， 3]$ D、 $[3 ， + \infty)$

查看试题解析
8. 已知实数 $x ､ y$ 满足 $\frac{1}{x} + \frac{1}{y} - 1 = 0$ ，且 $x y > 0$ ，若不等式 $4 x + 9 y - t \geq 0$ 恒成立，则实数 $t$ 的最大值为（）

A、9 B、25 C、16 D、12

查看试题解析

二、多选题

9. 关于 $x$ 的一元二次不等式 $a x^{2} + b x + 1 > 0$ 的解集为 $(- 1 ， \frac{1}{2})$ ，则下列成立的是（）

A、 $a < 0$ B、 $a^{2} + b^{2} = 5$ C、关于 $x$ 的一元二次不等式 $b x^{2} + a x - 1 \geq 0$ 的解集为 $\emptyset$ D、函数 $f (x) = x^{a}$ 为其定义域上的减函数

查看试题解析
10. 有以下判断，其中是正确判断的有（）

A、 $f (x) = \frac{| x |}{x}$ 与 $g (x) = {\begin{array}{l} 1 ， x \geq 0 \\ - 1 ， x < 0 \end{array}$ 表示同一函数 B、函数 $y = f (x)$ 的图像与直线 $x = 1$ 的交点最多有1个 C、“ $a > b$ ”是“ $a c^{2} > b c^{2}$ ”的必要不充分条件 D、若 $f (x) = | x - 1 | - | x |$ ，则 $f (f (\frac{1}{2})) = 1$

查看试题解析
11. 下列函数中最小值为2的是（）

A、 $y = x + \frac{1}{x}$ B、 $y = \frac{x^{2}}{2} + \frac{2}{x^{2}}$ C、 $y = \sqrt{x^{2} + 4} + \frac{1}{\sqrt{x^{2} + 4}}$ D、 $y = 2 x^{2} - 4 x + 4$

查看试题解析
12. 给出下列4个命题：其中正确的序号是（）

A、若 $f (x) = x^{2} - 2 a x$ 在 $[1 ， + \infty)$ 上是增函数，则 $a = 1$ B、函数 $f (x) = 2^{x} - x^{2}$ 只有两个零点 C、函数 $y = 2^{| x - 1 |}$ 的图像关于直线 $x = 1$ 对称 D、在同一坐标系中，函数 $y = 2^{x}$ 与 $y = 2^{- x}$ 的图像关于 $y$ 轴对称

查看试题解析

三、填空题

13. 已知函数 $y = a - \frac{2}{2^{x} + 1}$ 为奇函数，则实数 $a =$

查看试题解析
14. 若函数 $y = 2^{x^{2} - 6 x + 10}$ 的定义域为 $[2 ， 5]$ ，则该函数的值域是.

查看试题解析
15. 已知 $f (x) = {\begin{array}{l} a \cdot x^{- 2} ， x > 1 ， \\ - x^{2} - a x - 5 ， x \leq 1 \end{array}$ 在区间 $(- \infty ， + \infty)$ 上是单调增函数，则a的取值范围为.

查看试题解析
16. 已知某种药物在血液中以每小时 $20 %$ 的比例衰减，现给某病人静脉注射了该药物 $3000 m g$ ，设经过 $x$ 小时后，药物在病人血液中的量为 $y m g$ .（参考数据： $l g 2 = 0.301$ ） $y$ 与 $x$ 的关系式为.当该药物在病人血液中的量保持在 $1800 m g$ 以上，才有疗效；而低于 $600 m g$ ，病人就有危险，要使病人没有危险，再次注射该药物的时间不能超过小时（精确到 $0.1$ ）.

查看试题解析

四、解答题

17. 已知函数 $g (x) = (a + 1)^{x - 2} + 1 (a > 0)$ 的图像恒过定点 $A$ ，且点 $A$ 又在函数 $f (x) = l o g_{\sqrt{3}} (x + a)$ 的图像上.

(1)、求 $a$ 的值；

(2)、已知 $- 1 \leq l o g_{\frac{1}{2}} x \leq 1$ ，求函数 $y = {(\frac{1}{4 a})}^{x - 1} - 4 {(\frac{1}{2 a})}^{x} + 2$ 的最大值和最小值.

查看试题解析
18. 已知 $f (x)$ 为R上的奇函数，当 $x > 0$ 时， $f (x) = x^{2} - 2 x$ ．

(1)、求 $f (0)$ 的值；

(2)、求 $f (x)$ 的解析式；

(3)、作出 $y = f (x)$ 的图象，并求当函数 $y = f (x)$ 与函数 $y = m$ 图象恰有三个不同的交点时，实数m的取值范围．

查看试题解析
19. 已知集合 $A = {x | a - 2 \leq x \leq a + 1}$ ，集合 $B$ 为函数 $f (x) = \sqrt{(2 + x) (2 - x)}$ 的定义域.

(1)、当 $a = 4$ 时，求 $A \cup B$ ；

(2)、若______，求实数 $a$ 的取值范围.
在① $A ∩ B = A$ ；②“ $x ∈ B$ ”是“ $x ∈ A$ ”的必要不充分条件；③ $A \cap B = \emptyset$ ，这三个条件中任选一个，补充到本题第（2）问的横线处，并解答.（注：如果选择多个条件分别解答，按第一个解答计分.）

查看试题解析
20. 已知函数 $f (x) = l o g_{a} \frac{2 + x}{2 - x}$ （ $a > 0$ 且 $a \neq 1$ ）.

(1)、求函数的定义域；

(2)、判断 $f (x)$ 的奇偶性并证明；

(3)、已知函数 $f (x) \geq 0$ ，求 $x$ 的取值范围.

查看试题解析
21. 用打点滴的方式治疗“新冠”病患时，血药浓度（血药浓度是指药物吸收后，在血浆内的总浓度，单位： $m g / m l$ ）随时间（单位：小时）变化的函数符合 $c_{1} (t) = \frac{m_{0}}{150} (1 - 2^{- k t})$ ，其函数图象如图所示，其中 $m_{0}$ 为药物进入人体时的速率，k是药物的分解或排泄速率与当前浓度的比值.此种药物在人体内有效治疗效果的浓度在 $4 m g / m l$ 到 $15 m g / m l$ 之间，当达到上限浓度时（即浓度达到 $15 m g / m l$ 时），必须马上停止注射，之后血药浓度随时间变化的函数符合 $c_{2} (t) = c \cdot 2^{- k t}$ ，其中c为停药时的人体血药浓度. （结果保留小数点后一位，参考数据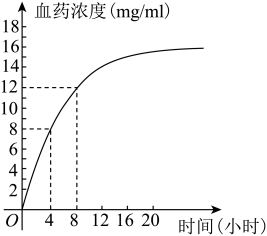： $l g 2 \approx 0.3 ， l g 15 \approx 1.18$ ）

(1)、求出函数 $c_{1} (t)$ 的解析式；

(2)、一病患开始注射后，最多隔多长时间停止注射？为保证治疗效果，最多再隔多长时间开始进行第二次注射？

查看试题解析
22. 已知函数 $f (x) = x^{2} + (m - 2) x - m$ ， $g (x) = \frac{f (x)}{x}$ ，且函数 $y = f (x - 2)$ 是偶函数．

(1)、求 $g (x)$ 的解析式；

(2)、若不等式 $g (l n x) - n l n x \geq 0$ 在 $[\frac{1}{e^{2}} ， 1)$ 上恒成立，求 $n$ 的取值范围；

(3)、若函数 $y = g (l o g_{2} (x^{2} + 4)) + k \cdot \frac{2}{l o g_{2} (x^{2} + 4)} - 9$ 恰好有三个零点，求 $k$ 的值及该函数的零点

查看试题解析

$t$	$2.0$	$3.0$	$4.0$	$5.1$	$6.18$
$v$	$1.5$	$4.02$	$7.5$	12	$18.3$