湖南省娄底市新化县五校联盟2022-2023学年高一上学期数学期末联考试卷
试卷更新日期:2023-02-03 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 设 , ,那么 是 的( )A、充分不必要条件 B、必要不充分条件 C、必要条件 D、既不充分也不必要条件3. 某工厂近期要生产一批化工试剂,经市场调查得知,生产这批试剂的成本分为以下三个部分:①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的费用是每单位元(试剂的总产量为单位,),则要使生产每单位试剂的成本最低,试剂总产量应为( )A、60单位 B、70单位 C、80单位 D、90单位4. 若函数的定义域为 , 则的取值范围是( )A、 B、 C、 D、5. 当时,在同一坐标系中,函数与的图象是( )A、
 B、
B、 C、
C、 D、
D、 6. 若将函数f(x)=sin2x+cos2x的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )A、 B、 C、 D、7. 已知函数的部分图象如图所示,点 , , 则下列说法错误的是( )
6. 若将函数f(x)=sin2x+cos2x的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )A、 B、 C、 D、7. 已知函数的部分图象如图所示,点 , , 则下列说法错误的是( )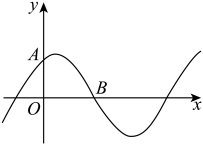 A、直线是图象的一条对称轴 B、的最小正周期为 C、在区间上单调递增 D、的图象可由向左平移个单位而得到8. 已知偶函数的图象经过点 , 且当时,不等式恒成立,则使得成立的取值范围为( )A、 B、 C、 D、
A、直线是图象的一条对称轴 B、的最小正周期为 C、在区间上单调递增 D、的图象可由向左平移个单位而得到8. 已知偶函数的图象经过点 , 且当时,不等式恒成立,则使得成立的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 定义集合运算: ,设 , ,则( )A、当 , 时, B、 可取两个值, 可取两个值, 有4个式子 C、 中有4个元素 D、 的真子集有7个10. 要得到的图象 , 只要将图象怎样变化得到A、将的图象沿x轴方向向左平移个单位 B、将的图象沿x轴方向向右平移个单位 C、先作关于x轴对称图象 , 再将图象沿x轴方向向右平移个单位 D、先作关于x轴对称图象 , 再将图象沿x轴方向向左平移个单位11. 德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 ,被称为狄利克雷函数.以下说法正确的是( ).A、 的值域是 B、 ,都有 C、存在非零实数 ,使得 D、对任意 ,都有12. 设函数 , 已知 在 有且仅有5个零点.下述四个结论中正确的是( )A、 在 有且仅有 个最大值点 B、 在 有且仅有2个最小值点 C、 在 单调递增 D、 的取值范围是
三、填空题
-
13. 已知命题 :“ , ”,则 为 .14. 已知 , , , 则的最大值是.15. 某堆雪在融化过程中,其体积(单位:)与融化时间(单位:)近似满足函数关系:(为常数),其图像如图所示.记此堆雪从融化开始到结束的平均融化速度为.那么中,瞬时融化速度等于的时刻是图中的.
 16. 已知函数在区间上单调,且对任意实数x均有成立,则φ=
16. 已知函数在区间上单调,且对任意实数x均有成立,则φ=四、解答题
-
17. 已知集合 ,集合 .(1)、当 时,求 ;(2)、若 ,求实数 的取值范围.18. 某单位建造一间地面面积为的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度不超过 米,房屋正面的造价为400元 , 房屋侧面的造价为 150元 , 屋顶和地面的造价费用合计为 元.(1)、把房屋总造价表示成的函数,并写出该函数的定义域.(2)、当侧面的长度为多少时,总造价最低,最低总造价是多少?19. 已知函数在轴右边的一部分图象如图所示.
 (1)、判断函数奇偶性并证明,作出函数在轴左边的图象.(2)、判断函数在上的单调性,并用单调性定义加以证明.
(1)、判断函数奇偶性并证明,作出函数在轴左边的图象.(2)、判断函数在上的单调性,并用单调性定义加以证明.