广东省东莞市2022-2023学年高一上学期数学期末试卷

试卷更新日期：2023-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. 命题“ $\exists x \in (0 ， + \infty)$ ， $\frac{1}{x} + 1 < 0$ ”的否定为（）

A、 $\exists x \in (0 ， + \infty)$ ， $\frac{1}{x} + 1 \geq 0$ B、 $\exists x \notin (0 ， + \infty)$ ， $\frac{1}{x} + 1 < 0$ C、 $\forall x \in (0 ， + \infty)$ ， $\frac{1}{x} + 1 \geq 0$ D、 $\forall x \in (0 ， + \infty)$ ， $\frac{1}{x} + 1 < 0$

查看试题解析
2. 函数 $f (x) = 2^{x} + 2 x - 7$ 的零点所在的区间为（）

A、 $(1 ， 2)$ B、 $(2 ， 3)$ C、 $(3 ， 4)$ D、 $(4 ， 5)$

查看试题解析
3. 已知全集 $U = {0 ， 1 ， 2 ， 3 ， 4 ， 5}$ ，集合 $A = {0 ， 2 ， 4 ， 5}$ ，集合 $B = {2 ， 3 ， 4}$ ，则如图所示的阴影部分表示的集合为（）

A、 ${2 ， 4}$ B、 ${0 ， 3 ， 5}$ C、 ${0 ， 1 ， 3 ， 5}$ D、 ${0 ， 2 ， 3 ， 4 ， 5}$

查看试题解析
4. 下列四组函数，表示同一个函数的一组是（）

A、 $y = \sqrt{x^{2}}$ ， $y = (\sqrt{x})^{2}$ B、 $y = l g 1 0^{x}$ ， $y = 1 0^{l g x}$ C、 $y = s i n | x |$ ， $y = | s i n x |$ D、 $y = x$ ， $y = \frac{x^{3} + x}{x^{2} + 1}$

查看试题解析
5. 记某时钟的中心点为 $O$ ，分针针尖对应的端点为 $A$ ．已知分针长 $O A = 5 c m$ ，且分针从12点位置开始绕中心点 $O$ 顺时针匀速转动．若以中心点 $O$ 为原点，3点和12点方向分别为 $x$ 轴和 $y$ 轴正方向建立平面直角坐标系，则点 $A$ 到 $x$ 轴的距离 $y$ （单位： $c m$ ）与时间t（单位：min）的函数解析式为（）

A、 $y = 5 | s i n t |$ B、 $y = 5 | c o s t |$ C、 $y = 5 | s i n \frac{π}{30} t |$ D、 $y = 5 | c o s \frac{π}{30} t |$

查看试题解析
6. “ $a < - 2$ ”是“ $f (x) = x + \frac{a}{x}$ 在 $(0 ， + \infty)$ 上单调递增”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 在不考虑空气阻力的情况下，火箭的最大速度 $v ($ 单位 $： k m / s$ ）和燃料的质量 $M$ （单位 $： k g$ ）、火箭（除燃料外）的质量 $m$ （单位： $k g$ ）的函数关系是 $v = a l g (1 + \frac{M}{m})$ （ $a$ 是参数）．当质量比 $\frac{M}{m}$ 比较大时，函数关系中真数部分的1可以忽略不计，按照上述函数关系，将质量比 $\frac{M}{m}$ 从2000提升至50000，则 $v$ 大约增加了（附： $l g 2 \approx 0.3010$ ）（）

A、52% B、42% C、32% D、22%

查看试题解析
8. 已知定义在 $R$ 上的函数 $f (x)$ 满足① $f (x) = | x | (- 1 \leq x \leq 1)$ ；② $f (x) = f (x + 2)$ ，则函数 $f (x)$ 与 $g (x) = {\begin{array}{l} 2^{x} ， & x \leq 0 \\ l o g_{\frac{1}{2}} x ， & x > 0 \end{array}$ 的图象在区间［－3，3]上的交点个数为（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、多选题

9. 下列命题为真命题的是（）

A、若 $a c > b c$ ，则 $a > b$ B、若 $a > b$ ， $c < 0$ ，则 $a c < b c$ C、若 $a > b$ ， $c > d$ ，则 $a c > b d$ D、若 $a > b$ 且 $\frac{1}{a} > \frac{1}{b}$ ，则 $a b < 0$

查看试题解析
10. 下列大小关系正确的是（）

A、 $3^{- 0.2} > {(\frac{1}{3})}^{0.4}$ B、 $3 l n 2 < 2 l n 3$ C、 $\sqrt{3} - \sqrt{2} > \sqrt{2} - 1$ D、 $s i n 1 > c o s 1$

查看试题解析
11. 狄利克雷函数是一个经典的函数，其解析式为 $f (x) = {\begin{array}{l} 1 ， x \in Q \\ 0 ， x \in ∁_{R} Q \end{array}$ ，则下列关于狄利克雷函数的结论正确的是（）

A、 $f (x)$ 的值域是 $[0 ， 1]$ B、 $\forall x \in R ， f (f (x)) = 1$ C、 $f (x)$ 是偶函数 D、 ${x | f (x) < \frac{1}{2}} = {x | f (x) > \frac{1}{2}}$

查看试题解析
12. 已知函数 $f (x) = \frac{s i n x}{| t a n x |}$ ，则下列结论正确的是（）

A、 $f (x)$ 的图像关于 $(π ， 0)$ 中心对称 B、 $f (x)$ 的最小正周期为 $π$ C、 $f (x)$ 在区间 $(\frac{π}{2} ， π)$ 上单调递增 D、 $f (x)$ 的值域为 $(- 1 ， 1)$

查看试题解析

三、填空题

13. 函数f(x)＝ $\sqrt{2^{x} - 1}$ ＋ $\frac{1}{x - 2}$ 的定义域为

查看试题解析
14. 已知 $s i n x - c o s x = \frac{1}{5}$ ，则 $s i n 2 x =$ ．

查看试题解析
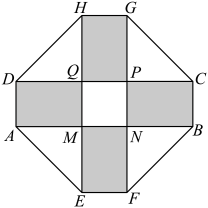
15. 已知函数 $f (x) = x - 8$ ， $g (x) = 3 x - x^{2}$ ， $x \in R$ ，用 $m (x)$ 表示 $f (x)$ ， $g (x)$ 中的较小者，记为 $m (x) = m i n {f (x) ， g (x)}$ ，则函数 $m (x)$ 的最大值为．

查看试题解析
16. 某公园设计了一座八边形的绿化花园，它的主体造型平面图（如图2）是由两个相同的矩形ABCD和EFGH构成的面积为 $80 m^{2}$ 的十字型区域，计划在正方形MNPQ上建一座花坛，造价为99元/ $m^{2}$ ；在四个空角（图中四个三角形）上铺草坪，造价为8元/ $m^{2}$ ；在四个矩形（图中阴影部分）上不做任何设计．设总造价为S（单位：元），AD长为x（单位：m），则绿化花园总造价S的最小值为元．

查看试题解析

四、解答题

17. 已知集合 $A = {x | x^{2} - 2 x - 3 \geq 0}$ ， $B = {y | y = x^{2} - 2 x - 3}$ ，

(1)、求A，B；

(2)、 $A \cup B$ ， $A \cap B$ ， $A ∩ (∁_{R} B)$ ．

查看试题解析
18. 已知 $α$ ， $β \in (0 ， \frac{π}{2})$ ， $c o s α = \frac{3}{5}$ ， $c o s β = \frac{5}{13}$ ．

(1)、求 $\frac{s i n (\frac{π}{2} - α) + c o s (\frac{3 π}{2} - α)}{s i n (3 π + α) + c o s (π - α)}$ 的值；

(2)、求 $s i n (α + β)$ 的值．

查看试题解析
19. 已知函数 $f (x) = l n x$ ．

(1)、若m＝f（3），n＝f（4），求 $e^{\frac{3 m - 2 n}{2}}$ 的值；

(2)、求不等式 $f (x - 2) < 2$ 的解集；

(3)、记函数 $F (x) = f (\frac{x - 1}{x + 1})$ ，判断 $F (x)$ 的奇偶性并证明．

查看试题解析
20. 已知函数 $f (x) = \sqrt{3} s i n x c o s x + c o s^{2} x + m$ ．

(1)、求 $f (x)$ 的单调递减区问；

(2)、若 $f (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上的最大值为 $\frac{1}{2}$ ，求使 $f (x) \geq 0$ 成立的 $x$ 的取值集合．

查看试题解析
21. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，当 $x \geq 0$ 时， $f (x) = 1 - a \cdot 2^{x}$ ．

(1)、求 $a$ 的值；

(2)、求 $f (x)$ 在 $R$ 上的解析式；

(3)、若函数 $g (x) = f (x) - k \cdot 2^{x}$ 有零点，求实数 $k$ 的取值范围．

查看试题解析
22. 如图，已知一块足球场地的球门 $M N$ 宽 $7$ 米，底线 $M N$ 上有一点 $A$ ，且 $A N$ 长 $9$ 米．现有球员带球沿垂直于底线的线路 $B A$ 向底线 $M A$ 直线运球，假设球员射门时足球运动线路均为直线．

(1)、当球员运动到距离点 $A$ 为 $4$ 米的点 $C$ 时，求该球员射门角度 $∠ M C N$ 的正切值；

(2)、若该球员将球直接带到点 $A$ ，然后选择沿其左后 $6 0^{∘}$ 方向（即 $∠ M A D = 6 0^{∘}$ ）的线路 $A D$ 将球回传给点 $D$ 处的队友．已知 $A D$ 长 $14$ 米，若该队友沿着线路 $D A$ 向点 $A$ 直线运球，并计划在线路 $D A$ 上选择某个位置 $E$ 进行射门，求 $A E$ 的长度多大时，射门角度 $∠ M E N$ 最大．

查看试题解析