2023年中考数学复习考点一遍过——相交线与平行线
试卷更新日期:2023-02-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
 A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角2. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )
A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角2. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )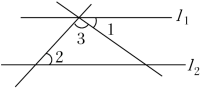 A、46° B、90° C、96° D、134°3. 已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )
A、46° B、90° C、96° D、134°3. 已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )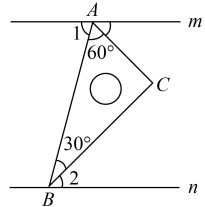 A、30° B、40° C、60° D、70°4. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
A、30° B、40° C、60° D、70°4. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )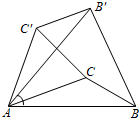 A、①②③ B、①②④ C、①③④ D、②③④5. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A、①②③ B、①②④ C、①③④ D、②③④5. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( ) A、27° B、53° C、57° D、63°6. 下列尺规作图不能得到平行线的是( )A、
A、27° B、53° C、57° D、63°6. 下列尺规作图不能得到平行线的是( )A、 B、
B、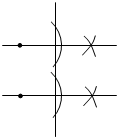 C、
C、 D、
D、 7. 如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角 , 则的度数为( )
7. 如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角 , 则的度数为( ) A、 B、 C、 D、8. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
A、 B、 C、 D、8. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )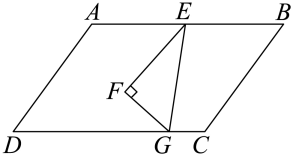 A、100° B、80° C、70° D、60°9. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( )
A、100° B、80° C、70° D、60°9. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( ) A、40° B、60° C、80° D、100°10. 如图,AB是⊙O的弦,OC⊥AB,垂足为C, , OC=OD,则∠ABD的度数为( )
A、40° B、60° C、80° D、100°10. 如图,AB是⊙O的弦,OC⊥AB,垂足为C, , OC=OD,则∠ABD的度数为( ) A、90° B、95° C、100° D、105°
A、90° B、95° C、100° D、105°二、填空题(每题3分,共24分)
-
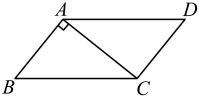
11. 如图,在中, , 若 , 则的度数是.
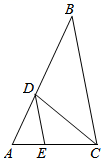
 12. 如图,在中, , , , 点是边上的一点,过点作 , 交于点 , 作的平分线交于点 , 连接.若的面积是2,则的值是.
12. 如图,在中, , , , 点是边上的一点,过点作 , 交于点 , 作的平分线交于点 , 连接.若的面积是2,则的值是.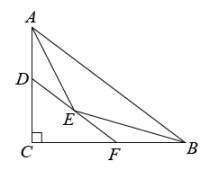 13. 一副三角板如图放置, , , , 则 .
13. 一副三角板如图放置, , , , 则 . 14. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 .
14. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 . 15. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .
15. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .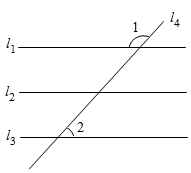 16. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.
16. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.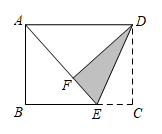 17. 如图,在中,弦半径 , 则的度数为 .
17. 如图,在中,弦半径 , 则的度数为 .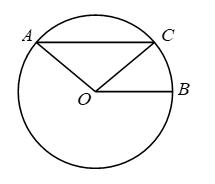 18. 如图,在等腰直角三角形中, , 点M,N分别为 , 上的动点,且 , .当的值最小时,的长为.
18. 如图,在等腰直角三角形中, , 点M,N分别为 , 上的动点,且 , .当的值最小时,的长为.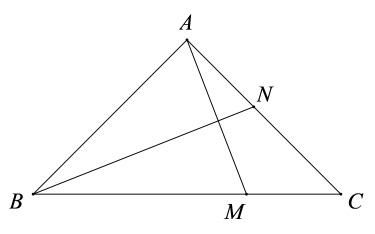
三、解答题(共8题,共66分)
-
19. 填空并完成以下证明:
如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.

解:∠AED与∠C的大小关系是 .
证明:∵∠1+∠2=180°(已知)
∠1=∠DFH( )
∴ =180°
∴EH∥AB( )
∴∠3=∠ADE( )
∵∠3=∠B
∴∠B=∠ADE( )
∴ ∥BC( )
∴∠AED=∠C( )
20. 如图, , 直线分别与直线、直线相交于点E,F,点G在上,平分 . 若 , 求的度数. 21. 如图,、分别在、上,是的中点, , 求证: .
21. 如图,、分别在、上,是的中点, , 求证: . 22. 如图,C为∠AOB平分线上一点,点D在射线OA上,且OD=CD.
22. 如图,C为∠AOB平分线上一点,点D在射线OA上,且OD=CD.求证:CD∥OB.
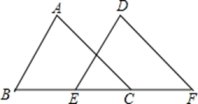
 23. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
23. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.