山西省阳泉市高新区2022-2023学年七年级上学期期末教学质量线上检测数学试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，最大的有理数是（）

A、-1 B、0 C、-3 D、0.08

查看试题解析
2. 下列计算结果正确的是（）

A、 $2 + (- 5) = - 7$ B、 ${(- 1)}^{2020} = - 2020$ C、 $(- 2) \times (- 4) = 8$ D、 ${(- 4)}^{2} = 8$

查看试题解析
3. 如图是由若干个相同的小正方体搭成的一个几何体分别从正面，左面，上面看到的形状图．则组成这个几何体的小正方体的个数为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 若一个角的余角的 $3$ 倍比这个角的补角多12°，则这个角的度数为（）

A、 $38 °$ B、 $39 °$ C、 $40 °$ D、 $41 °$

查看试题解析
5. 下列等式成立的是（）

A、 $3 y^{2} - (- 2 y^{2}) = 5 y^{2}$ B、 $5 x + 5 y = 10 x y$ C、 $6 y^{2} - 2 y^{2} = 4$ D、 $4 a^{2} b - 4 a b^{2} = 0$

查看试题解析
6. 如图，数轴上的点 $A$ ，点 $B$ 分别表示有理数 $a$ ， $b$ ．下列式子错误的是（）

A、 $a + b < 0$ B、 $a b < 0$ C、 $| a | - | b | > 0$ D、 $b - | a | < 0$

查看试题解析
7. 圆柱形可口可乐易拉罐的底面半径为 $3 c m$ ，高为 $10 c m$ ，里面装满了可口可乐（罐的厚度不计）．打开 $8$ 罐可口可乐倒入一个底面半径为 $10 c m$ ，高为 $12 c m$ 的圆柱形电饭锅中准备加热，求电饭锅中可口可乐的液面离电饭锅上边沿多少 $c m$ ．设电饭锅中可口可乐的液面离电饭锅上边沿 $x c m$ ．可列方程（）

A、 $3^{2} π \times 10 \times 8 = 1 0^{2} π (12 - x)$ B、 $3^{2} π \times 10 \times 8 = 1 0^{2} π x$ C、 $3 \times 10 \times 8 π = 10 π (12 - x)$ D、 $10 \times 8 \times 6 π = 20 π (12 - x)$

查看试题解析
8. 十八大以来，山西省省委、省政府不断加大支农政策力度，加大财政和全社会的投入，充分调动广大农民务农种粮积极性，全省粮食生产再上新台阶．据国家统计局山西省调查总队统计数据，十八大期间，山西省全省年均粮食生产总量达到129.92亿千克.129.92亿用科学记数法表示为（）

A、 $129.92 \times 1 0^{8}$ B、 $129.92 \times 1 0^{9}$ C、 $1.2992 \times 1 0^{9}$ D、 $1.2992 \times 1 0^{10}$

查看试题解析
9. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“信”字所在面相对面上的汉字是（）

A、阳 B、光 C、诚 D、实

查看试题解析
10. 某电器商场购进一批冰箱，每台进价为2000元，为了促进销售，商场决定所有商品按标价八折再减80元销售，若想按这种方式销售每台冰箱仍能获利 $10 %$ ，该冰箱的标价应是（）

A、2280 B、2850 C、2880 D、3000

查看试题解析

二、填空题

11. 用四舍五入法对287.449取近似数，要求精确到0.1，其结果为．

查看试题解析
12. 木工师傅在锯木料时，一般先在木料上画出两个点，然后过这两个点弹出一条墨线，这是因为.

查看试题解析
13. 重阳节前夕，某校七年级二班45名同学到敬老院进行文艺演出，项目有独唱、合唱和诗朗诵，要求每人只能参加一项．已知，合唱人数是独唱人数的3倍，诗朗诵的人数比合唱人数少4人．设参加独唱的有 $x$ 人，可列方程：．

查看试题解析
14. 如图，点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 在线段 $M N$ 上，则图中共有条线段．

查看试题解析
15. 相传大禹在治洛水的时候，洛水神龟献给大禹一本洛书，书中有一幅奇怪的图（如图所示），这幅图用今天的符号翻译出来，就是一个三阶幻方，也就是在 $3 \times 3$ 的方阵中填入9个数，每行、每列和每条对角线上的数字和相等．我们定义：在 $3 \times 3$ 的方阵图中，每行、每列和每条对角线上的数字和都相等，称为三阶幻方．下图为三阶幻方的一部分，图中“？”代表的有理数是．

查看试题解析

三、解答题

16.

(1)、计算： $3 \div (- \frac{1}{2}) - (\frac{2}{5} - \frac{1}{3}) \times 15$

(2)、计算： ${(- 3)}^{2} - {(- 2)}^{3} \times (- \frac{1}{4}) - (- 1 + 6)$

(3)、先化简，再求值： $3 (a^{2} - 4 a) - (- 2 a + 4 a^{2})$ ，其中 $a = - 1$ ．

查看试题解析
17. 解方程：

(1)、 $5 x + 6 = 2 (x - 3)$ ；

(2)、 $\frac{x - 1}{3} - \frac{2 x + 1}{4} = 1$

查看试题解析
18. 如图，在同一平面内有三个点 $A$ ， $B$ ， $C$ ．

(1)、利用尺规，按下面的要求作图．要求：不写画法，保留作图痕迹，不必写结论；
①作射线 $B A$ ；
②作线段 $B C$ ；
③连接 $A C$ ，并在线段 $A C$ 上作一条线段 $A D$ ，使 $A D = A B$ ，连接 $B D$ ．

(2)、观察（1）题得到的图形，请直接写出 $D B + D C$ 与 $B C$ 的大小关系是．

查看试题解析
19. 小明在学习了正方体的展开图后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀剪开了一个长方体纸盒，可是一不小心多剪开了一条棱，把纸盒剪成了两部分，如图1、图2所示．请根据你所学的知识，回答下类问题：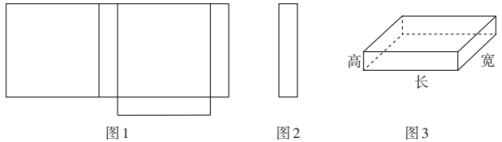
观察判断：
小明共剪开了 ▲ 条棱；
动手操作：
现在小明想将剪断的图2重新粘贴到图1上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒（如图3），请你帮助小明在图1中补全图形：
解决问题：
经过测量，小明发现这个纸盒的底面是一个正方形，其边长是长方体的高的5倍，并且纸盒所有棱长的和是 $880 c m$ ，求这个纸盒的体积．

查看试题解析
20. 随着 $5 G$ 时代的来临，张老师换了新发布的 $5 G$ 手机并且需要新办一种 $5 G$ 套餐．运营商提出了两种包月套餐方案，第一种是每50元月租费，流量资费 $0.4 元 / G B$ ；第二种是没有月租费，但流量资费 $0.6 元 / G B$ ．设张老师每月使用流量 $x G B$ ．

(1)、张老师按第一种套餐每月需花费元，按第二种套餐每月需花费元；（用含x的代数式表示）

(2)、若张老师这个月使用流量 $200 G B$ ，通过计算说明哪种套餐比较合算：

(3)、张老师每月使用多少流量时，两种套餐花费一样多?

查看试题解析
21. 学校为表彰“2021迎新越野赛”的运动员，购买了20个笔袋，30个笔筒，60个圆规作为奖品，共花费1020元．已知，每个笔袋比圆规贵9元，每个笔筒的单价是圆规单价的2倍．这三种奖品的单价各是多少元？

查看试题解析
22. 如图：

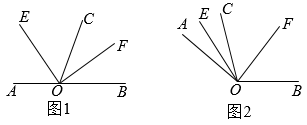(1)、如图1所示，点O是直线 $A B$ 上一点， $O E$ 平分 $∠ A O C$ ， $O F$ 平分 $∠ B O C$ ，请直写出 $∠ E O F$ 的度数为；

(2)、如图2所示，射线 $O C$ 在 $∠ A O B$ 内部，且 $∠ A O B = 140 °$ ， $O E$ 平分 $∠ A O C$ ， $O F$ 平分 $∠ B O C$ ，求 $∠ E O F$ 的度数；

(3)、观察（1）（2）的条件与计算结果，直接写出你发现的结论：；

(4)、若 $∠ A O B = 140 °$ ，射线 $O C$ 在 $∠ A O B$ 的外部， $O E$ 平分 $∠ A O C$ （ $∠ A O C$ 小于平角）， $O F$ 平分 $∠ B O C$ （ $∠ B O C$ 小于平角），直接写出 $∠ E O F$ 的度数为．

查看试题解析
23. 综合与探究
课堂情境：数轴是规定了原点、正方向和单位长度的直线．任何有理数都可以用数轴上的点表示．数轴上表示一个数的点到原点的距离叫做这个数的绝对值．数轴上右边的数总比左边的数大…根据这些性质，我们可以借助数轴解决很多问题
今天我们研究数轴上两点之间的距离与这两个有理数之间的关系，
观察发现：

(1)、填空：如图所示，在数轴上，有理数 $5$ 与 $2$ 对应的两点之间的距离为；
在数轴上，有理数 $6$ 与 $- 1$ 对应的两点之间的距离为；
在数轴上，有理数 $- 1$ 与 $- 5$ 对应的两点之间的距离为；
答疑解惑：
小明提出：在数轴上，有理数-4与-1对应的两点之间的距离可以写为 $- 4 - (- 1)$ 吗？
小亮回答：不可以．两点之间的距离不能是负数．两个点之间的距离应该写成这两个数的差的绝对值；
小慧回答：不可以．两个点之间的距离等于右边的数减去左边的数

(2)、方法验证：
观察数轴上给出的两点之间距离，选用小亮或小慧的方法求数轴上两点之间距离；
$A B =$ ； $E F =$ ； $A C =$ ； $D E =$ ；

(3)、解决问题：
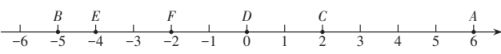
若点 $P$ 从点 $A$ 出发以每秒2个单位长度的速度向左运动，同时点 $Q$ 从点 $B$ 出发以每秒1个单位长度的速度向右运动，求经过多长时间 $P$ ， $Q$ 两点之间的距离为2个单位长度？

查看试题解析