山西省吕梁市汾阳市2022-2023学年七年级上学期期末考试数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、- C、-3 D、32. 如图,这是一个正方体的表面展开图,则原正方体中与“瞰”字所在的面相对的字是( )
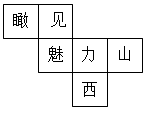 A、魅 B、力 C、山 D、西3. 大熊猫的历史可谓源远流长,迄今所发现的最古老的大熊猫成员——始熊猫,其化石出土于我国云南禄丰和元谋两地,地质年代约为800万年前中新世晚期.数据800万用科学记数法可表示为( )A、 B、 C、 D、4. 如图,从标有单项式的四张卡片中找出所有能合并的同类项,若它们合并后的结果为 , 则代数式的值为( )
A、魅 B、力 C、山 D、西3. 大熊猫的历史可谓源远流长,迄今所发现的最古老的大熊猫成员——始熊猫,其化石出土于我国云南禄丰和元谋两地,地质年代约为800万年前中新世晚期.数据800万用科学记数法可表示为( )A、 B、 C、 D、4. 如图,从标有单项式的四张卡片中找出所有能合并的同类项,若它们合并后的结果为 , 则代数式的值为( )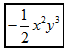
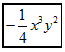
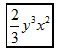
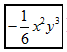 A、-1 B、0 C、1 D、25. 方程 去括号变形正确的是( )A、 B、 C、 D、6. 如图,已知点位于点南偏东30°的方向上,若 , 在的左侧,则点位于点( )
A、-1 B、0 C、1 D、25. 方程 去括号变形正确的是( )A、 B、 C、 D、6. 如图,已知点位于点南偏东30°的方向上,若 , 在的左侧,则点位于点( ) A、南偏西的方向上 B、南偏东的方向上 C、北偏东的方向上 D、北偏西的方向上7. “居家嗨购,网上过年”,为做好疫情防控并促进春节消费,山西省组织开展了2022年“全晋乐购”网上年货节活动,某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工,该企业选购了甲种物品件,单价是100元;乙种物品件,单价是240元.则该企业共花费在( )A、元 B、元 C、元 D、元8. 如图, , 为的中点,点在线段上,且 , 则的长度是( )
A、南偏西的方向上 B、南偏东的方向上 C、北偏东的方向上 D、北偏西的方向上7. “居家嗨购,网上过年”,为做好疫情防控并促进春节消费,山西省组织开展了2022年“全晋乐购”网上年货节活动,某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工,该企业选购了甲种物品件,单价是100元;乙种物品件,单价是240元.则该企业共花费在( )A、元 B、元 C、元 D、元8. 如图, , 为的中点,点在线段上,且 , 则的长度是( ) A、 B、 C、 D、9. 《九章算术》是我国古代的第一部自成体系的数学专著,其中的许多数学问题是世界上记载最早的,《九章算术》卷七“盈不足”有如下记载:今有共买琎,人出半,盈四;人出少半,不足三.问人数、进价各几何?译文:今有人合伙买琎石,每人出钱,会多4钱;每人出钱,又差3钱,问人数和进价各是多少?设人数为 , 则依据题意,下列方程正确的为( )
A、 B、 C、 D、9. 《九章算术》是我国古代的第一部自成体系的数学专著,其中的许多数学问题是世界上记载最早的,《九章算术》卷七“盈不足”有如下记载:今有共买琎,人出半,盈四;人出少半,不足三.问人数、进价各几何?译文:今有人合伙买琎石,每人出钱,会多4钱;每人出钱,又差3钱,问人数和进价各是多少?设人数为 , 则依据题意,下列方程正确的为( ) A、 B、 C、 D、10. 下图所示的地板图案是由若干个大小相同的长方形按规律组成的,第1个图案由4个长方形组成;第2个图案由7个长方形组成;第3个图案由10个长方形组成;第4个图案由13个长方形组成;…;若按此规律排列,第2022个图案中长方形的个数为( )
A、 B、 C、 D、10. 下图所示的地板图案是由若干个大小相同的长方形按规律组成的,第1个图案由4个长方形组成;第2个图案由7个长方形组成;第3个图案由10个长方形组成;第4个图案由13个长方形组成;…;若按此规律排列,第2022个图案中长方形的个数为( ) A、6065 B、6066 C、6067 D、6068
A、6065 B、6066 C、6067 D、6068二、填空题
-
11. 如果电梯上升2层记作层,那么下降3层记作层.12. 已知 , 则.13. 已知x=2是关于的方程的解,则a的值是 .14. 将一副三角板按如图所示的方式摆放,若 , 则的度数为 .
 15. 现定义一种新运算,对于任意有理数 , , , 满足 , 若对于含未知数的式子满足 , 则x= .
15. 现定义一种新运算,对于任意有理数 , , , 满足 , 若对于含未知数的式子满足 , 则x= .三、解答题
-
16.(1)、计算: .(2)、解方程: .17. 如图,已知直线 , 相交于点 , . 若 , 求的度数.
 18. 下面是小明同学化简整式的过程,请仔细阅读并完成相应任务.
18. 下面是小明同学化简整式的过程,请仔细阅读并完成相应任务.计算:
.
任务:
(1)、以上化简步骤中,第步开始出现错误.(2)、请你写出该整式正确的化简过程.19. “抗击疫情,人人有责”,我省某校对全校师生进行体温检测.下面是其中8位老师的体温检测结果表(规定:超过规定体温36.5的记为“+”,不足规定体温36.5的记为“-”)
序号
1
2
3
4
5
6
7
8
体温/
+0.4
+0.6
+0.1
0
-0.2
-0.1
+0.8
(1)、表中最高体温与最低体温的差是多少?并用“”将表中体温数值连接起来.(2)、已知人的正常体温范围是(包括36.2和37.2),那么这8位老师的体温属于正常范围的有几位?请说明理由.20. 我们规定,若关于的一元一次方程的解为 , 则称该方程为“差解方程”,例如:的解为2,且 , 则该方程是差解方程.请根据上述规定解答下列问题:(1)、判断是否是差解方程;(2)、若关于的一元一次方程是差解方程,求的值.21. 下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.年月日 星期日
制作长方体纸箱今天我在书店一本书上看到下面材料:
某工厂计划用100张白板纸制作某种型号的长方体纸箱,如图,每一张白板纸可以用A, , 三种方法裁前,其中A种裁法是将一张白板纸裁成4个侧面,种裁法是将一张白板纸裁成3个侧面和2个底面,种裁法是将一张白板纸裁成2个侧面和4个底面.那么利用材料中的4个侧面和2个底面恰好能做成一个纸箱.若设按A种方法裁剪的有张白板纸,按种方法裁剪的有张白板纸.

我有如下思考:……
(1)、按种方法裁剪的白板纸有( )A、张 B、张 C、张 D、张(2)、将这100张白板纸裁剪完后,用含 , 的代数式表示一共可以裁剪出多少个侧面和多少个底面,请说明理由.(结果要化简)(3)、当 , 时,最多可以制作该种型号的长方体纸箱个.22. 综合与探究如图,数轴上有一点从原点开始出发,先向左移动(1个单位长度表示)到达点,再向左移动到达点,然后向右移动到达点.
 (1)、请在题中所给的数轴上表示出 , , 三点的位置.(2)、把点到点的距离记为 , 则cm;若数轴上的点表示的数为 , 点表示的数为 , 则cm.(3)、若点以每秒的速度向左移动,同时点 , 分别以每秒、的速度向右移动,设移动时间为秒,试探究的值是否会随着的变化而变化,请说明理由.23. 如图,两条直线相交于点O,且 , 射线(与射线重合)绕点O逆时针方向旋转,速度为每秒 , 射线(与射线重合)绕点O顺时针方向旋转,速度为每秒 , 两射线 , 同时运动,运动时间为t秒(本题出现的角均指不大于平角的角).
(1)、请在题中所给的数轴上表示出 , , 三点的位置.(2)、把点到点的距离记为 , 则cm;若数轴上的点表示的数为 , 点表示的数为 , 则cm.(3)、若点以每秒的速度向左移动,同时点 , 分别以每秒、的速度向右移动,设移动时间为秒,试探究的值是否会随着的变化而变化,请说明理由.23. 如图,两条直线相交于点O,且 , 射线(与射线重合)绕点O逆时针方向旋转,速度为每秒 , 射线(与射线重合)绕点O顺时针方向旋转,速度为每秒 , 两射线 , 同时运动,运动时间为t秒(本题出现的角均指不大于平角的角).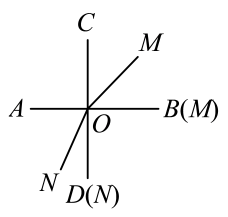 (1)、图中一定有个直角;当 , 的度数为;当 , 的度数为;(2)、当时,若 , 试求出t的值;(3)、当时,探究的值,在t满足怎样的条件时是定值,在t满足怎样的条件时不是定值?
(1)、图中一定有个直角;当 , 的度数为;当 , 的度数为;(2)、当时,若 , 试求出t的值;(3)、当时,探究的值,在t满足怎样的条件时是定值,在t满足怎样的条件时不是定值?