山西省临汾市2022-2023学年七年级上学期期末数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. -6的相反数为( )A、 B、6 C、-6 D、2. 下列运算结果正确的是( )A、 B、 C、 D、3. 某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“时”字所在面相对的面上的汉字是( )
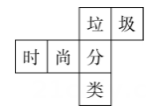 A、分 B、垃 C、圾 D、类4. 根据国家统计局统计,2022年前三季度,夏粮早稻实现增产,全国夏粮早稻产量合计3511亿斤,秋粮生产总体稳定,从收获的情况看,全年粮食有望再获丰收.数据“3511亿”用科学记数法表示为( )
A、分 B、垃 C、圾 D、类4. 根据国家统计局统计,2022年前三季度,夏粮早稻实现增产,全国夏粮早稻产量合计3511亿斤,秋粮生产总体稳定,从收获的情况看,全年粮食有望再获丰收.数据“3511亿”用科学记数法表示为( ) A、 B、 C、 D、5. 如图,能用 、 、 三种方法,表示同一个角的是( )A、
A、 B、 C、 D、5. 如图,能用 、 、 三种方法,表示同一个角的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,两条平行线a,b被第三条直线c所截.若 , 则的度数为( )
6. 如图,两条平行线a,b被第三条直线c所截.若 , 则的度数为( ) A、 B、 C、 D、7. 已知的相反数是-5,的倒数是 , 是多项式的次数,则的值为( )A、3 B、 C、1 D、-18. 把一副三角板与按如图所示方式摆放在一起,已知 , , 其中A,D,B三点在同一条直线上.若和分别是和的平分线,则的度数为( )
A、 B、 C、 D、7. 已知的相反数是-5,的倒数是 , 是多项式的次数,则的值为( )A、3 B、 C、1 D、-18. 把一副三角板与按如图所示方式摆放在一起,已知 , , 其中A,D,B三点在同一条直线上.若和分别是和的平分线,则的度数为( ) A、 B、 C、 D、9. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、
A、 B、 C、 D、9. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、 B、
B、 C、
C、 D、
D、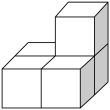 10. 在《九章算术注》中用不同颜色的算筹(注:小棍形状的记数工具)分别表示正数和负数(白色表示正数,黑色表示负数),图1所表示的是的计算过程,则图2所表示的是( )
10. 在《九章算术注》中用不同颜色的算筹(注:小棍形状的记数工具)分别表示正数和负数(白色表示正数,黑色表示负数),图1所表示的是的计算过程,则图2所表示的是( )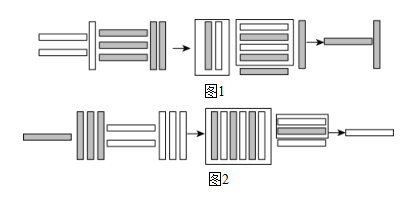 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
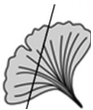
11. 计算:-6+5= .12. 金秋十月,不仅是丰收的季节,而且到处是色彩斑斓的景色,太原市迎泽公园藏着银杏叶极致的风景.小明同学捡到一片沿直线被折断了的银杏叶(如图),他发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
 13. 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC,∠AOC=40°,则∠DOE的度数为 .
13. 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC,∠AOC=40°,则∠DOE的度数为 .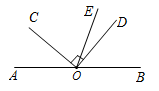 14. 如图是一组有规律的图案,它们是由正三角形组成的,第1个图案中有6个正三角形,第2个图案中有10个正三角形,第3个图案中有14个正三角形……按此规律,第n个图案中有个正三角形.(用含的代数式表示)
14. 如图是一组有规律的图案,它们是由正三角形组成的,第1个图案中有6个正三角形,第2个图案中有10个正三角形,第3个图案中有14个正三角形……按此规律,第n个图案中有个正三角形.(用含的代数式表示) 15. 如图,C,D是线段AB上两点,且点C在点D的左侧,M,N分别是线段 , 的中点.若 , , 则AB的长为 .
15. 如图,C,D是线段AB上两点,且点C在点D的左侧,M,N分别是线段 , 的中点.若 , , 则AB的长为 .
三、解答题
-
16.(1)、计算:;(2)、先化简,再求值: , 其中 , .17. 如图,将方格纸中的图形先向右平行移动5格,再向下平行移动4格,画出平行移动后的图形.
 18. 阅读下面的解答过程,并填空.
18. 阅读下面的解答过程,并填空.如图, , 平分 , 平分 , . 求证: .

证明:∵平分 , 平分 , (已知)
∴ ▲ , ▲ . (角平分线的定义)
又∵ , (已知)
∴∠ ▲ =∠ ▲ . (等量代换)
又∵ , (已知)
∴∠ ▲ ∠ ▲ . (等量代换)
∴ . ( )
19. 某原料仓库某一天的原料进出记录如下表(运进用正数表示,运出用负数表示):进出数量(单位:吨)
-2
3
-1
2
-4
进出次数
2
1
3
4
2
(1)、这天仓库的原料比原来增加了还是减少了?请说明理由.(2)、根据实际情况,现有两种方案:方案一:运进每吨原料费用6元,运出每吨原料费用9元;
方案二:不管运进还是运出费用都是每吨7元.
从节约运费的角度考虑,请说明选择哪种方案比较合适.
20. 如图,点C在射线上,于点F. (1)、使用圆规和直尺作图:(要求:保留作图痕迹,不写作法)
(1)、使用圆规和直尺作图:(要求:保留作图痕迹,不写作法)在射线上画出点E,使C为线段的中点,连接 .
(2)、连接 , 在线段 , , 中,线段最短,依据是 .(3)、若 , 求的度数.21. 如图,长方形的长为m,宽为n,扇形的半径为n,的长为 . (1)、求图中阴影部分的面积S.(用含m,n的代数式表示)(2)、当 , 时,求S的值.(结果保留)22. 阅读材料:
(1)、求图中阴影部分的面积S.(用含m,n的代数式表示)(2)、当 , 时,求S的值.(结果保留)22. 阅读材料:定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的 , 则称该点是其他两个点的“倍分点”.例如,数轴上点A,B,C所表示的数分别为–1,0,2,且满足 , 则点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.
 (1)、基础巩固:在A,B,C三点中,点是点M,N的“倍分点”.(2)、尝试应用:若数轴上点M是点A,D的“倍分点”,则点D在数轴上对应的数有个.(3)、灵活运用:若数轴上点N是点P,M的“倍分点”,且点Р在点N的右侧,求此时点Р在数轴上表示的数.23. 综合与实践
(1)、基础巩固:在A,B,C三点中,点是点M,N的“倍分点”.(2)、尝试应用:若数轴上点M是点A,D的“倍分点”,则点D在数轴上对应的数有个.(3)、灵活运用:若数轴上点N是点P,M的“倍分点”,且点Р在点N的右侧,求此时点Р在数轴上表示的数.23. 综合与实践问题情境:
数学活动课上,老师展示了一个问题:如图1,直线 , 直线与 , 分别交于点C,D,点A在直线上,且在点C的左侧,点B在直线上,且在点D的左侧,点Р是直线上的一个动点(点Р不与点C,D重合).当点Р在点C,D之间运动时,试猜想 , , 之间的数量关系,并说明理由.
独立思考:
 (1)、请解答老师提出的问题.实践探究:
(1)、请解答老师提出的问题.实践探究:勤学小组对此问题进行了更深一步的思考:当点Р在C,D两点的外侧运动时, , , 之间的数量关系又是如何?
(2)、如图2,当点P运动到点C上方时,试猜想 , , 之间的数量关系,并说明理由.(3)、如图3,当点P运动到点D下方时,请直接写出 , , 之间的数量关系.