山西省2022-2023学年七年级上学期期末综合评估数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，比 $- 2$ 小的数是（）

A、-1 B、0 C、-3 D、1

查看试题解析
2. 下列调查中，最适合采用抽样调查的是（）

A、了解我校七年级（1）班全体同学的视力情况 B、乘坐飞机时对旅客行李的检查 C、了解小林家五口人对春节来历的知晓程度 D、了解某批LED灯的使用寿命

查看试题解析
3. 在人体血液中，每立方毫米血液里有5000000个红细胞．数据5000000用科学记数法表示为（）

A、 $50 \times 1 0^{5}$ B、 $5 \times 1 0^{6}$ C、 $0.5 \times 1 0^{7}$ D、 $5 \times 1 0^{7}$

查看试题解析
4. 如图，这是一个正方体的表面展开图，六个面上各有一字，连起来是“全面落实双减”，把它折成正方体后，与“落”相对的字是（）

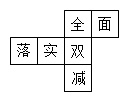A、面 B、实 C、双 D、减

查看试题解析
5. 某学校随机选取了若干名学生进行“我最喜欢的球类运动”的调查，并将调查结果绘制成如图所示的扇形统计图．已知最喜欢网球的学生有40人，则下列说法错误的是（）

A、这次被调查的学生共400人 B、扇形统计图中羽毛球部分的扇形的圆心角的度数为 $72 °$ C、喜欢网球、羽毛球和乒乓球的学生人数占总人数的一半 D、被调查的学生中喜欢羽毛球的学生有80人

查看试题解析
6. 小华在解关于x的方程 $\frac{x + 4}{3} - \frac{x + k}{4} = 2$ “去分母”步骤时，等号右边的“2”忘记乘以12，他求得的解为 $x = 1$ ，则k的值为（）

A、5 B、-5 C、2 D、-15

查看试题解析
7. 将无限循环小数 $0 . \overset{\cdot}{7}$ 化为分数，可以设 $0 . \overset{\cdot}{7} = x$ ，则 $10 x = 7 + x$ ，解得 $x = \frac{7}{9}$ ．仿此，将无限循环小数 $0 . \overset{\cdot}{2} \overset{\cdot}{1}$ 化为分数的结果为（）

A、 $\frac{7}{11}$ B、 $\frac{7}{33}$ C、 $\frac{21}{101}$ D、 $\frac{20}{99}$

查看试题解析
8. 已知过 $m$ 边形的一个顶点有3条对角线，正 $n$ 边形的边长为5，周长为40，则 $n - m$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 如图，在一条笔直的大道上有A，B，C三个小区，O为A，C区的中点．已知某校学生中，住在A区有3人，B区有2人，C区有6人，且 $A C = 1000 m$ ， $B C = 700 m$ ．若学校将O处作为校车的停靠点，则这些学生从住处到该停靠点的路程之和是（）

A、 $4400 m$ B、 $4900 m$ C、 $5400 m$ D、 $5800 m$

查看试题解析
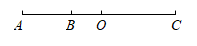10. 如图，在同一平面内， $∠ A O B = 90 °$ ，若 $∠ A O C = ∠ B O D = 30 °$ ，则 $∠ C O D$ 的度数不可能为（）

A、 $30 °$ B、 $90 °$ C、 $120 °$ D、 $150 °$

查看试题解析

二、填空题

11. 想要了解本周天气的变化情况，最适合采用统计图(填“扇形”、“折线”或“条形”)．

查看试题解析
12. 若 $- 5 x^{4} y$ 与 $- 37 x^{2 m} y^{n}$ 是同类项，则mn= ．

查看试题解析
13. 某车间生产一批圆柱形机器零件，从中抽出了6件进行检验，把标准直径的长记为0，比标准直径长的记为正数，比标准直径短的记为负数，检查记录如下：
序号
1
2
3
4
5
6
与标准直径的差值
+0.2
+0.4
-0.3
+0.3
-0.1
-0.2
则第个零件最符合标准．

查看试题解析
14. 甲、乙、丙三根木棒按如图所示的位置摆放在地面上．已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲没有与乙重叠的部分的长度为 $3 m$ ，丙没有与乙重叠的部分的长度为 $5 m$ ．若甲的长度为 $a m$ ，乙的长度为 $b m$ ，则丙的长度为 $m$ ．（用含有 $a$ 、 $b$ 的代数式表示）

查看试题解析
15. 由一些相同的立方体小木块搭建成的几何体，从正面、从左面和从上面看的形状图如图所示，则该几何体是由块小木块搭建而成的．

查看试题解析

三、解答题

16. 计算与解方程：

(1)、计算： $| \frac{1}{3} - \frac{2}{3} | \div (- \frac{1}{12}) - \frac{1}{8} \times {(- 2)}^{3}$ ；

(2)、解方程： $\frac{x + 2}{4} - \frac{2 x - 3}{6} = 1$ ．

查看试题解析
17. 先化简，再求值： $(2 x^{2} - 5 x) - (3 x^{2} - 4 x + 2) + x^{2}$ ，其中 $x = - \frac{1}{2}$ ．

查看试题解析
18. 对于有理数a，b，n，d，若 $| a - n | + | b - n | = d$ ，则称a和b关于n的“相对距离”为d，例如， $| 2 - 1 | + | 3 - 1 | = 3$ ，则2和3关于1的“相对距离”为3．

(1)、 $- 3$ 和4关于1的“相对距离”为．

(2)、若a和5关于2的“相对距离”为6，求a的值．

查看试题解析
19. 一辆货车从超市出发，向东走了1千米到达小明家，继续向东走了3千米到达小兵家，然后向西走了10千米到达小华家，最后又回到超市结束行程．

(1)、如果以超市为原点，以向东为正方向，用1个单位长度表示1千米，请你在数轴上表示出小明家、小兵家和小华家的具体位置．

(2)、可小华家离小兵家多远？

(3)、若货车每千米耗油0.13升，则这次行程货车共耗油多少升？

查看试题解析
20. 观察下列等式．
第1个等式 $2^{2} - 1^{2} = 2 \times 1 + 1$ ；
第2个等式 $3^{2} - 2^{2} = 2 \times 2 + 1$ ；
第3个等式 $4^{2} - 3^{2} = 2 \times 3 + 1$ ；
第4个等式 $5^{2} - 4^{2} = 2 \times 4 + 1$ ；
……
按照以上规律，解决下列问题：

(1)、第5个等式为．

(2)、猜想第n个等式为（用含n的式子表示）．

(3)、观察下列各图，“·”的个数用a表示，“○”的个数用b表示，如：当 $n = 1$ 时， $a = 4$ ， $b = 1$ ；当 $n = 2$ 时， $a = 9$ ， $b = 4$ ；当 $n = 3$ 时， $a = 16$ ， $b = 9$ ；…当 $n = 2023$ 时，求 $a - b$ 的值．

查看试题解析
21. 某校为了了解七年级800名学生跳绳情况，从七年级学生中随机抽取部分学生进行1分钟跳绳测试，并对测试成绩进行统计分析，得到如下所示的频数分布表：
跳绳个数 $(n)$
$0 < n \leq 100$
$100 < n \leq 120$
$120 < n \leq 140$
$140 < n \leq 160$
$160 < n \leq 200$
频数
16
30
50
$a$
24
所占百分比
8%
15%
25%
40%
$b$
请根据尚未完成的表格，解答下列问题：

(1)、本次随机抽取了名学生进行1分钟跳绳测试，表中a= ， b=；

(2)、补全频数直方图；

(3)、若绘制“七年级学生1分钟跳绳测试成绩扇形统计图”，则测试成绩在 $120 < n \leq 140$ 个所对应扇形的圆心角的度数是；

(4)、若跳绳个数超过140个为优秀，则该校七年级学生1分钟跳绳成绩优秀的约有多少人？

查看试题解析
22. 综合与实践
为响应国家节能减排的号召，引导节能低碳行为，某市居民生活用电实行“阶梯收费”标准，标准如下：
居民月用电量/千瓦时
单价/元
不超过 $180$ 千瓦时
a
超过 $180$ 千瓦时但不超过 $350$ 千瓦时的部分
0.65
超过 $350$ 千瓦时的部分
0.9
已知小贤家三月份用电 $150$ 千瓦时，电费为 $90$ 元．

(1)、上表中a= ．

(2)、若小贤家七月份用电370千瓦时，求小贤家七月份的电费．

(3)、若小贤家八月份电费为286元，求小贤家八月份的用电量．

查看试题解析
23. 综合与探究

(1)、特例感知：如图1，线段 $A B = 16 c m$ ， C为线段AB上的一个动点，点D，E分别是AC，BC的中点．
①若 $A C = 4 c m$ ，则线段DE的长为cm．
②设 $A C = a c m$ ，则线段DE的长为cm．

(2)、知识迁移：我们发现角的很多规律和线段一样，如图2，若 $∠ A O B = 120 °$ ， OC是 $∠ A O B$ 内部的一条射线，射线OM平分 $∠ A O C$ ，射线ON平分 $∠ B O C$ ，求 $∠ M O N$ 的度数．

(3)、拓展探究：已知 $∠ C O D$ 在 $∠ A O B$ 内的位置如图3所示， $∠ A O B = α$ ， $∠ C O D = 30 °$ ，且 $∠ D O M = 2 ∠ A O M$ ， $∠ C O N = 2 ∠ B O N$ ，求 $∠ M O N$ 的度数．（用含 $α$ 的代数式表示）

查看试题解析

序号	1	2	3	4	5	6
与标准直径的差值	+0.2	+0.4	-0.3	+0.3	-0.1	-0.2

跳绳个数 $(n)$	$0 < n \leq 100$	$100 < n \leq 120$	$120 < n \leq 140$	$140 < n \leq 160$	$160 < n \leq 200$
频数	16	30	50	$a$	24
所占百分比	8%	15%	25%	40%	$b$

居民月用电量/千瓦时	单价/元
不超过 $180$ 千瓦时	a
超过 $180$ 千瓦时但不超过 $350$ 千瓦时的部分	0.65
超过 $350$ 千瓦时的部分	0.9