山东省青岛市市南区2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的倒数是（　　）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
2. 下列图形中，不是正方体的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
3. 如图的几何体，其左视图是（）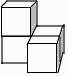

A、 B、 C、 D、

查看试题解析
4. 某数学兴趣小组为了解本校有多少学生已经患上近视，制定了四种抽样调查方案，你认为比较合理的调查方案是（）

A、在校门口通过观察统计有多少学生； B、在低年级学生中随机抽取一个班进行调查； C、从每个年级的每个班随机抽取1名男生进行调查； D、随机抽取本校每个年级10%的学生进行调查．

查看试题解析
5. 半径为1的圆中，扇形 $A O B$ 的圆心角为 $120 °$ ，则扇形 $A O B$ 的面积为（）

A、 $\frac{π}{6}$ B、 $\frac{2 π}{3}$ C、 $\frac{π}{3}$ D、 $π$

查看试题解析
6. 若 $- 3 x^{2 m} y^{3}$ 与 $2 x^{4} y^{n}$ 是同类项．则|m-n|的值是（）

A、0 B、1 C、7 D、－1

查看试题解析
7. 如图，把一块长为45cm，宽为25cm的矩形硬纸板的四角减去四个相同的小正方形，然后把纸板沿虚线折起，做成一个无盖纸盒．若该无盖纸盒的底面积为625cm² ，设剪去小正方形的边长为xcm，则可列方程为（）

A、 $(45 - 2 x) (25 - x) = 625$ B、 $(45 - x) (25 - x) = 625$ C、 $(45 - x) (25 - 2 x) = 625$ D、 $(45 - 2 x) (25 - 2 x) = 625$

查看试题解析
8. 通过观察下面每个图形的规律，得出第四个图形中 $y$ 的值是（）

A、12 B、-12 C、-9 D、15

查看试题解析

二、填空题

9. 据报道，春节期间微信红包收发高达3270000000次，数字3270000000用科学记数法表示为

查看试题解析
10. 甲、乙两家汽车销售公司根据近几年的销售量，分别制作了如下折线统计图，试判断：从2014年到2018年，这两家公司中销售量增长较快的是公司．

查看试题解析
11. 下午3：40，时针和分针的夹角是．

查看试题解析
12. 某商场将一件玩具按进价提高50%后标价，销售时按标价打八折销售，结果相对于进价仍获利20元，则这件玩具的进价是元.

查看试题解析
13. 直线l上有三点A、B、C，其中 $A B = 8 c m$ ， $B C = 6 c m$ ， M、N分别是 $A B$ 、 $B C$ 的中点则 $M N$ 的长是．

查看试题解析
14. 观察一列单项式： $a ， - 2 a^{2} ， 4 a^{3} ， - 8 a^{4} ， . . .$ 根据你发现的规律，第7个单项式为；第n个单项式为．

查看试题解析
15. 如图是某校七（2）班45名同学入学语文成绩统计表．现要制作频数直方图来反映这个班语文成绩的分布情况，若以10分为组距分组，共可分组．
语文成绩/分
46
59
66
72
人数（频数）
1
2
3
4
语文成绩/分
74
79
82
83
人数（频数）
2
3
3
4
语文成绩/分
85
86
87
88
人数（频数）
5
2
4
3
语文成绩/分
91
92
94
98
人数（频数）
2
3
3
1

查看试题解析
16. 如图所示的三阶幻方，其对角线、横行、纵向的和都相等，则根据所给数据，可以确定这个和为．

2
10
-6

查看试题解析

三、解答题

17. 用圆规、直尺作图，不写作法，但要保留作图痕迹．
已知：线段 $a$ ， $b$ ．求作：线段 $M N$ ，使 $M N = 2 b - a$ ．

查看试题解析
18. 计算：

(1)、 $(- \frac{5}{6} + \frac{3}{4}) \times (- 48)$ ；

(2)、 $- 1^{4} + 16 \div {(- 2)}^{3} - (- \frac{1}{8}) \times 4$ ．

查看试题解析
19. 先化简，再求值： $- 2 (m n - 3 m^{2}) + (m n - m^{2})$ ，其中 $m = - 2$ ， $n = - 3$ ．

查看试题解析
20. 解方程：

(1)、 $2 (100 - 15 x) = 60 + 5 x$ ；

(2)、 $\frac{x - 7}{4} - \frac{5 x + 8}{3} = 1$ ．

查看试题解析
21. 某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在A处，规定向北方向为正，当天行驶情况记录如下（单位：千米）：+10，﹣8，+7，﹣15，+6，﹣16，+4，﹣2

(1)、A处在岗亭何方？距离岗亭多远？

(2)、若摩托车每行驶1千米耗油0.5升，这一天共耗油多少升？

查看试题解析
22. 如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠AOC和∠COB的度数．

查看试题解析
23. 为了解某品牌冰箱销售量的情况，销售人员对某商场十月份该品牌甲、乙、丙三种型号的冰箱销售量进行统计，绘制如下两个统计图（均不完整）．请你结合图中的信息，解答下列问题：

(1)、该商场十月份售出这种品牌的冰箱共多少台？

(2)、补全条形统计图；

(3)、在扇形统计图中，求出乙种冰箱部分所对应的圆心角的度数；

(4)、若该商场计划订购这三种型号的冰箱共1600台，根据十月份销售量的情况，求该商场应订丙种型号的冰箱多少台比较合理？

查看试题解析
24. 某通讯公司有两种移动电话计费方式，如下表：

月使用费用（元）
主叫限定时间（分）
主叫超时费（分）
被叫
方式一
58
150
$0.25$
免费
方式二
88
350
$0.19$
免费

(1)、如果一个月主叫时间为350分钟，则方式一需支付的费用是元；由此可以判断出一个月主叫时间等于或者大于350分钟时，选择方式费用较少；

(2)、如果设一个月主叫时间为x（ $x > 150$ ）分钟，则方式一需支付的费用为（用x表示）；

(3)、有没有可能两种方式一个月支付的费用一样多？如果有，请求出主叫时间；如果不能，请说明理由．

查看试题解析
25. 七年级1班共有学生45人，其中男生比女生少3人．某节课上，老师组织同学们做圆柱形笔筒．每名学生每节课能做筒身30个或筒底90个．

(1)、七年级1班有男生、女生各多少人？

(2)、原计划女生负责做筒身，男生做筒底，要求每个筒身匹配2个筒底，那么每节课做出的筒身和筒底配套吗？如果不配套，男生要支援女生几人，才能使筒身和筒底配套？（列方程解决问题）

查看试题解析
26. 如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

(1)、写出数轴上点B表示的数；点P表示的数（用含t的代数式表示）

(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？

(3)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速到家动，若点P、Q同时出发，问点P运动多少秒时追上Q？

(4)、若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．

查看试题解析

语文成绩/分	46	59	66	72
人数（频数）	1	2	3	4
语文成绩/分	74	79	82	83
人数（频数）	2	3	3	4
语文成绩/分	85	86	87	88
人数（频数）	5	2	4	3
语文成绩/分	91	92	94	98
人数（频数）	2	3	3	1

	月使用费用（元）	主叫限定时间（分）	主叫超时费（分）	被叫
方式一	58	150	$0.25$	免费
方式二	88	350	$0.19$	免费