吉林省长春市德惠市2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数,若其意义相反,则分别叫做正数与负数.若向东走9米记作+9米,则-5米表示( )A、向东走5米 B、向西走5米 C、向东走4米 D、向西走4米2. 航天科技集团所研制的天问一号探测器由长征五号运载火箭发射,并成功着陆于火星,距离地球约192000000千米.其中192000000用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体的展开图中,能围成圆柱的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,射线表示的方向是( )
4. 如图,射线表示的方向是( ) A、东偏南 B、南偏东 C、北偏西 D、南偏东5. 下列图形中,根据 , 能得到的是( )A、
A、东偏南 B、南偏东 C、北偏西 D、南偏东5. 下列图形中,根据 , 能得到的是( )A、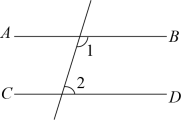 B、
B、 C、
C、 D、
D、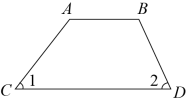 6. 如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
6. 如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( ) A、两点之间,线段最短 B、两点确定一条直线 C、过一点,有无数条直线 D、连接两点之间的线段叫做两点间的距离7. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:① ;② ;③ ;④ .其中正确的是( )
A、两点之间,线段最短 B、两点确定一条直线 C、过一点,有无数条直线 D、连接两点之间的线段叫做两点间的距离7. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:① ;② ;③ ;④ .其中正确的是( ) A、①③ B、③④ C、①② D、②④8. 如图,点A是直线l外一点,过点A作于点B.在直线l上取一点C,连接 , 使 , 点P在线段上,连接 , 若 , 则线段的长不可能是( )
A、①③ B、③④ C、①② D、②④8. 如图,点A是直线l外一点,过点A作于点B.在直线l上取一点C,连接 , 使 , 点P在线段上,连接 , 若 , 则线段的长不可能是( )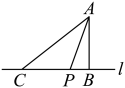 A、3.5 B、4.1 C、5 D、5.5
A、3.5 B、4.1 C、5 D、5.5二、填空题
-
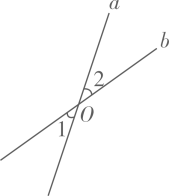
9. 若单项式与是同类项,则m= .10. 若一个角的大小为 , 则这个角的补角的大小为 .11. 如图,直线a、b交于点O,若 , 则 .
 12. 小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费 元.
12. 小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费 元.
 13. 如图,若 , M为的中点, , 则的长度为 .
13. 如图,若 , M为的中点, , 则的长度为 . 14. 定义一种新运算:“”观察下列各式:
14. 定义一种新运算:“”观察下列各式:, 则(用含a、b的代数式表示)
三、解答题
-
15. 计算(1)、(2)、16. 先化简,再求值: , 其中 , .17. 如图是由棱长都为的6块小正方体组成的简单几何体.

请在方格中画出该几何体的三个视图.
18. 超市购进8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,-3,2,-0.5,1,-2,-2,-2.5.(1)、这8筐白菜总计超过或不足多少千克?(2)、超市计划这8筐白菜按每千克3元销售,为促销超市决定打九折销售,求这8筐白菜现价比原价便宜了多少钱?19. 小亮对家中客厅的窗户设计了两种窗帘,图1的窗帘是由两个完全相同的四分之一圆组成,图2的窗帘是由一个半圆和两个四分之一圆组成(半径相同). (1)、如图1所示的窗帘,用代数式表示窗户能射进阳光的面积是(结果保留π).(2)、通过计算说明图1、图2哪种设计使窗户能射进阳光的面积更大?大多少?(结果保留π)20. 填空:(将下面的推理过程及依据补充完整)如图,
(1)、如图1所示的窗帘,用代数式表示窗户能射进阳光的面积是(结果保留π).(2)、通过计算说明图1、图2哪种设计使窗户能射进阳光的面积更大?大多少?(结果保留π)20. 填空:(将下面的推理过程及依据补充完整)如图,已知:平分 , , , 那么平分吗?

解:∵平分(已知),
∴ ▲ ( ),
∵(已知),
∴ ▲ ,
∴(等量代换),
∵ ▲ (已知),
∴( ),
( ),
∴ ▲ (等量代换).
∴平分 .
21. 如图①是我省同金电力科技有限公司生产的美利达自行车的实物图,图②是它的部分示意图, , 点在上, , , .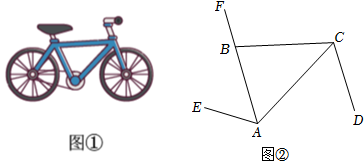 (1)、请分别写出图中以点为顶点的角有 .(2)、试求和的度数.22. 如图,将一副直角三角板的直角顶点C叠放在一起.
(1)、请分别写出图中以点为顶点的角有 .(2)、试求和的度数.22. 如图,将一副直角三角板的直角顶点C叠放在一起. (1)、若 , 则;若 , 则;(2)、猜想∠ACB与∠DCE的大小有何特殊关系?并说明理由.(3)、若 , 求∠DCE的度数.23. 【感知】如图1, , , , 求的度数.
(1)、若 , 则;若 , 则;(2)、猜想∠ACB与∠DCE的大小有何特殊关系?并说明理由.(3)、若 , 求∠DCE的度数.23. 【感知】如图1, , , , 求的度数.小明的思路是:过点P作 , 通过平行线性质来求 .
 (1)、按小明的思路,易求得∠APC的度数为度;(直接写出答案)(2)、【探究】如图2, , 点P在射线上运动,记 , , 当点P在B、D两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、【迁移】在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),试着探究与、之间的数量关系是否会发生变化,请从下面①和②中挑选一种情形,画出图形,写出结论,并说明理由.
(1)、按小明的思路,易求得∠APC的度数为度;(直接写出答案)(2)、【探究】如图2, , 点P在射线上运动,记 , , 当点P在B、D两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、【迁移】在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),试着探究与、之间的数量关系是否会发生变化,请从下面①和②中挑选一种情形,画出图形,写出结论,并说明理由.①点P在线段上;
②点P在射线上.
24. 如图,P是线段AB上任一点,AB=12cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2cm/s,D点的运动速度为3cm/s,运动的时间为ts. (1)、若AP=8cm,
(1)、若AP=8cm,①运动1s后,求CD的长;
②当D在线段PB上运动时,试说明AC=2CD;
(2)、如果t=2s时,CD=1cm,试探索AP的值.