吉林省白城市大安市2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 在-8,-1,1,0这四个数中,最大的数是( )A、-8 B、-1 C、1 D、02. 的倒数是( )A、3 B、 C、-3 D、3. 火星和地球的距离约为34 000 000千米,用科学记数法表示34 000 000的结果是( )千米.A、0.34×108 B、3.4×106 C、34×106 D、3.4×1074. 如图是由几个相同的小正方体堆砌成的几何体,从上面看到该几何体的形状图是( )
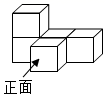 A、
A、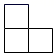 B、
B、 C、
C、 D、
D、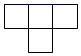 5. 将方程 移项后,正确的是( )A、 B、 C、 D、6. 利用一副三角板上已知度数的角,不能画出的角是( )A、15° B、100° C、165° D、135°
5. 将方程 移项后,正确的是( )A、 B、 C、 D、6. 利用一副三角板上已知度数的角,不能画出的角是( )A、15° B、100° C、165° D、135°二、填空题
-
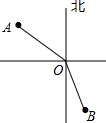
7. 我市某天最高气温是15℃,最低气温是零下3℃,那么当天的最大温差是℃.8. 多项式是四次项式9. 如果与的和为单项式,那么b的值是 .10. 要在墙上订牢一根木条,至少需要2颗钉子,其理由是 .11. 如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB= .
 12. 如图,点C、D在线段上, , 若 , 则 .
12. 如图,点C、D在线段上, , 若 , 则 . 13. 某种家电商场将一种品牌的电脑按标价的9折出售,仍可获利1800元,已知该品牌电脑进价为9000元,如果设该电脑的标价为x元,根据题意得到的方程是 .14. 如图,观察所给算式,找出规律:
13. 某种家电商场将一种品牌的电脑按标价的9折出售,仍可获利1800元,已知该品牌电脑进价为9000元,如果设该电脑的标价为x元,根据题意得到的方程是 .14. 如图,观察所给算式,找出规律:1+2+1=4,
1+2+3+2+1=9,
1+2+3+4+3+2+1=16,
1+2+3+4+5+4+3+2+1=25,
……
根据规律计算1+2+3+…+99+100+99+…+3+2+1=
三、解答题
-
15. 计算16. 解方程17. 已知互为相反数,互为倒数,的绝对值是 , 求 .18. 已知一个角的余角是这个角的补角的 ,求这个角的度数.19. 先化简,再求值: , 其中 ,20. 如图,是直线上的一点,为任一条射线,平分 , 平分 . 试说明与具有怎样的数量关系.
 21. 有一群鸽子和一些鸽笼,如果每个鸽笼6只鸽子,则剩余3只鸽子无鸽笼可住;如果在飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子.原来有多少只鸽子和鸽笼?22. 如图,已知直线l和直线外三点A,B,C,按下列要求画图:
21. 有一群鸽子和一些鸽笼,如果每个鸽笼6只鸽子,则剩余3只鸽子无鸽笼可住;如果在飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子.原来有多少只鸽子和鸽笼?22. 如图,已知直线l和直线外三点A,B,C,按下列要求画图:
⑴画射线
⑵连接
⑶延长至D,使得
23. 定义一种新运算“☆”,规则为:m☆n=mn+mn-n,例如:2☆3=23+2×3-3=8+6-3=11,解答下列问题:(1)、(-2)☆4;(2)、(-1)☆[(-5)☆2].24. 如图,线段 , 点M是的中点. (1)、求线段的长度;(2)、在上取一点N,使得 . 求的长.
(1)、求线段的长度;(2)、在上取一点N,使得 . 求的长.