河北省廊坊市广阳区2022-2023学年七年级上学期期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 小杨同学检测了4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准质量的是( )A、
 B、
B、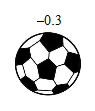 C、
C、 D、
D、 2. 下列各数: , , , 0, , ……,其中有理数的个数是( )A、2 B、3 C、4 D、53. 神舟十四号载人飞船是北京时间2022年6月5日10时44分由长征二号F遥十四运载火箭成功送入近地点高度200000米、远地点350000米、倾角42°的地球近地轨道.将350000用科学记数法表示应为( )A、 B、 C、 D、4. 有理数a,b,c在数轴上对应点的位置如图所示,下列说法正确的是( )
2. 下列各数: , , , 0, , ……,其中有理数的个数是( )A、2 B、3 C、4 D、53. 神舟十四号载人飞船是北京时间2022年6月5日10时44分由长征二号F遥十四运载火箭成功送入近地点高度200000米、远地点350000米、倾角42°的地球近地轨道.将350000用科学记数法表示应为( )A、 B、 C、 D、4. 有理数a,b,c在数轴上对应点的位置如图所示,下列说法正确的是( ) A、 B、 C、 D、5. 计算( )A、 B、 C、 D、6. 下列结论正确的是( )A、比大 B、单项式的次数是5 C、是方程的解 D、7. 若 , 则下列变形正确的是( )A、 B、 C、 D、8. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
A、 B、 C、 D、5. 计算( )A、 B、 C、 D、6. 下列结论正确的是( )A、比大 B、单项式的次数是5 C、是方程的解 D、7. 若 , 则下列变形正确的是( )A、 B、 C、 D、8. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、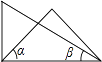 C、
C、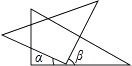 D、
D、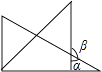 9. 如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
9. 如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )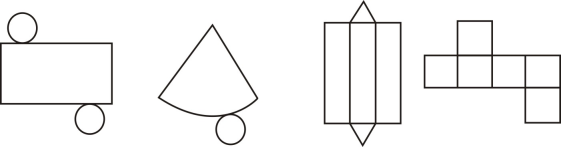 A、圆柱,圆锥,四棱柱,正方体 B、四棱锥,圆锥,正方体,圆柱 C、圆柱,圆锥,正方体,三棱锥 D、圆柱,圆锥,三棱柱,正方体10. 如图,数轴的单位长度为1,若点和点所表示的两个数的绝对值相等,则点表示的数是( )
A、圆柱,圆锥,四棱柱,正方体 B、四棱锥,圆锥,正方体,圆柱 C、圆柱,圆锥,正方体,三棱锥 D、圆柱,圆锥,三棱柱,正方体10. 如图,数轴的单位长度为1,若点和点所表示的两个数的绝对值相等,则点表示的数是( ) A、-3 B、-1 C、1 D、311. 如图, , C为的中点.点D在线段上,且 , 则的长度是( )
A、-3 B、-1 C、1 D、311. 如图, , C为的中点.点D在线段上,且 , 则的长度是( )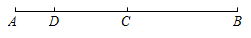 A、 B、 C、 D、12. 如图,已知 , 分别平分和 . 若 , , 则的度数为( )
A、 B、 C、 D、12. 如图,已知 , 分别平分和 . 若 , , 则的度数为( ) A、 B、 C、 D、13. 如果单项式与的和是单项式,那么的值为( )A、 B、0 C、-1 D、114. 如图,已知∠AOB与∠EO′F,分别以O,O′为圆心,以同样长为半径画弧,分别交OA,OB于点A′,B′,交O′E,O′F于点E′,F′,以B′为圆心,以E′F′长为半径画弧,交弧A′B′于点A″.下列结论错误的是( )
A、 B、 C、 D、13. 如果单项式与的和是单项式,那么的值为( )A、 B、0 C、-1 D、114. 如图,已知∠AOB与∠EO′F,分别以O,O′为圆心,以同样长为半径画弧,分别交OA,OB于点A′,B′,交O′E,O′F于点E′,F′,以B′为圆心,以E′F′长为半径画弧,交弧A′B′于点A″.下列结论错误的是( ) A、∠AOB=2∠EO′F B、∠AOB>∠EO′F C、∠A″OB=∠EO′F D、∠AOA″=∠AOB﹣∠EO′F15. 小嵩利用计算机设计了一个计算程序,输入和输出的数据如表:
A、∠AOB=2∠EO′F B、∠AOB>∠EO′F C、∠A″OB=∠EO′F D、∠AOA″=∠AOB﹣∠EO′F15. 小嵩利用计算机设计了一个计算程序,输入和输出的数据如表:输入
⋯
1
2
3
4
5
⋯
输出
⋯
⋯
那么,当输入数据是8时,输出的数据是( )
A、 B、 C、 D、16. 为响应习总书记“绿水青山,就是金山银山”的号召,某校今年3月争取到一批植树任务,领到一批树苗,按下列方法依次由各班领取:第一班领取全部的 , 第二班领取100棵和余下的 , 第三班领取200棵和余下的 , 第四班领取300棵和余下的……,最后树苗全部被领完,且各班领取的树苗数相等,则树苗总棵树为( )A、6400 B、8100 C、9000 D、4900二、填空题
-
17. 在2,-4,-5,6这四个数中,任取两个数相乘,所得的积最大是 .18. 如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是.
 19. 当时,代数式 .20. 如图是2005年5月份的日历,如图中那样,用一个圈竖着圈住3个数,如果被圈住的三个数的和为30,则这三个数最小一个所表示的日期为2005年5月日.
19. 当时,代数式 .20. 如图是2005年5月份的日历,如图中那样,用一个圈竖着圈住3个数,如果被圈住的三个数的和为30,则这三个数最小一个所表示的日期为2005年5月日.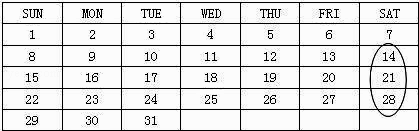
三、解答题
-
21.(1)、计算: .(2)、解方程: .(3)、先化简,再求值: , 其中 .22. 如图,已知、在线段上.
 (1)、图中共有条线段;(2)、若 .
(1)、图中共有条线段;(2)、若 .①比较线段的长短: ▲ (填“>”“=”或“<”);
②若 , , 是的中点,是的中点,求线段的长度.
 23. 甲乙两个粮仓仓库的粮食重量比是11:3,如果从甲仓库运15吨到乙仓库,那么甲、乙两仓库粮食重量比就是4:3,原来两个仓库各有粮食多少吨?24. 已知有下列两个代数式:①;② .(1)、当 , 时,代数式①的值是 , 代数式②的值是 .(2)、当 , 时,代数式①的值是;代数式②的值是 .(3)、观察(1)和(2)中代数式的值,你发现代数式和的关系为(用式子表示) .(4)、利用你发现的规律,求 .25. 已知点、、在同一条直线上, .
23. 甲乙两个粮仓仓库的粮食重量比是11:3,如果从甲仓库运15吨到乙仓库,那么甲、乙两仓库粮食重量比就是4:3,原来两个仓库各有粮食多少吨?24. 已知有下列两个代数式:①;② .(1)、当 , 时,代数式①的值是 , 代数式②的值是 .(2)、当 , 时,代数式①的值是;代数式②的值是 .(3)、观察(1)和(2)中代数式的值,你发现代数式和的关系为(用式子表示) .(4)、利用你发现的规律,求 .25. 已知点、、在同一条直线上, .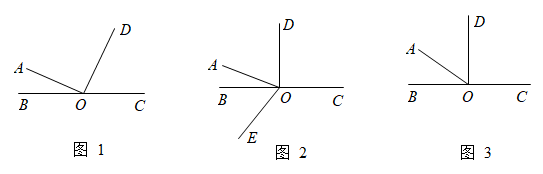 (1)、如图1,若 , , 则 .(2)、如图2,若 , , 平分 , 求 .(3)、如图3,若与互余,也与互余,请在图3中画出符合条件的射线加以计算后,写出的度数(用含的式子表示).26. 结合数轴与绝对值的知识回答下列问题:
(1)、如图1,若 , , 则 .(2)、如图2,若 , , 平分 , 求 .(3)、如图3,若与互余,也与互余,请在图3中画出符合条件的射线加以计算后,写出的度数(用含的式子表示).26. 结合数轴与绝对值的知识回答下列问题: (1)、探究:
(1)、探究:①数轴上表示5和2的两点之间的距离 .
②数轴上表示和的两点之间的距离是 .
③数轴上表示和4的两点之间的距离是 .
(2)、归纳:一般的,数轴上表示数和数的两点之间的距离等于 .
(3)、应用:①若数轴上表示数的点位于与3之间,则的值= .
②若表示数轴上的一个有理数,且 , 则a= .
③若表示数轴上的一个有理数,的最小值是 .
④若表示数轴上的一个有理数,且 , 则有理数的取值范围是 .
(4)、拓展:已知,如图2,、分别为数轴上的两点,点对应的数为 , 点对应的数为100.若当电子蚂蚁从点出发,以4个单位/秒的速度向右运动,同时另一只电子蚂蚁恰好从点出发,以3单位/秒的速度向左运动,求经过多长时间两只电子蚂蚁在数轴上相距20个单位长度,并写出此时点所表示的数.