广东省阳江市阳西县2022-2023学年七年级上学期期末考试数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 2023的相反数是( )A、 B、 C、2023 D、-20232. 2022年十三届全国人大五次会议审议通过的政府工作报告中提出,今年城镇新增就业目标为11000000人以上.数据11000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,某同学用剪刀沿虚线将三角形剪掉一个角,发现四边形的周长比原三角形的周长要小,能正确解释这一现象的数学知识是( )
 A、两点确定一条直线 B、点动成线 C、直线是向两端无限延伸的 D、两点之间,线段最短4. 下列是一元一次方程的是( )A、 B、 C、 D、5. 下列整式与为同类项的是( )A、 B、 C、 D、6. 下列运用等式性质进行的变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 已知 , 则的值为( )A、-4 B、0 C、4 D、-88. 一个角的补角比这个角的余角的3倍少 , 这个角为( )A、 B、 C、 D、9. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、
A、两点确定一条直线 B、点动成线 C、直线是向两端无限延伸的 D、两点之间,线段最短4. 下列是一元一次方程的是( )A、 B、 C、 D、5. 下列整式与为同类项的是( )A、 B、 C、 D、6. 下列运用等式性质进行的变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 已知 , 则的值为( )A、-4 B、0 C、4 D、-88. 一个角的补角比这个角的余角的3倍少 , 这个角为( )A、 B、 C、 D、9. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、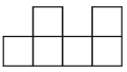 B、
B、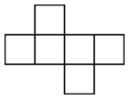 C、
C、 D、
D、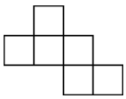 10. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )
10. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )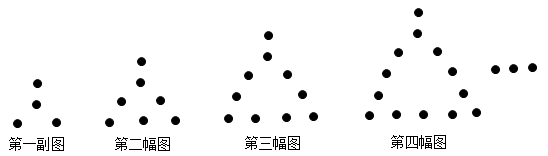 A、297 B、301 C、303 D、400
A、297 B、301 C、303 D、400二、填空题
-
11. 如果水位升高 时水位变化记作 ,那么水位下降 时水位变化记作 .12. 单项式的次数是 .13. 已知 , 则x+y= .14. 若关于x的方程的解是x=2,则a的值为 .15. 如图,已知轮船A在灯塔P的北偏东方向,轮船B在灯塔P的南偏东方向,则的度数是 .

三、解答题
-
16. 计算: .17. 解方程: .18. 先化简,再求值: , 其中 , .19. 出租车司机李师傅某天下午从停车场出发一直沿东西方向的大街进行营运,规定向东为正,向西为负,他的行驶里程(单位:)记录如下:
+10,-6,+3,+12,-12,+5,-13,5.
(1)、当把最后一名乘客送达目的地时,李师傅在停车场的什么位置?(2)、若每千米的营运额为3元,成本为1.5元 , 则这天下午他盈利多少元?20. 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降 .(1)、求明年每辆无人驾驶出租车的预计改装费用是多少万元;(2)、求明年改装的无人驾驶出租车是多少辆.21. 如图,已知线段 , , 点M是AC的中点. (1)、求线段AM的长;(2)、在CB上取一点N,使得 , 求线段MN的长.22. 已知内部有三条射线,其中,平分 , 平分 .
(1)、求线段AM的长;(2)、在CB上取一点N,使得 , 求线段MN的长.22. 已知内部有三条射线,其中,平分 , 平分 .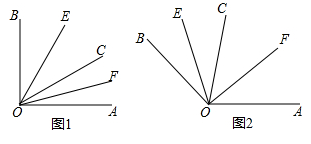 (1)、如图1,若 , , 求的度数;(2)、如图2,若 , 求的度数(用含的式子表示);(3)、若将题中的“平分”条件改为“ , ”,且 , 用含的式子表示的度数为 .23. 如图,已知数轴上A,B两点对应的数分别为 , 3.
(1)、如图1,若 , , 求的度数;(2)、如图2,若 , 求的度数(用含的式子表示);(3)、若将题中的“平分”条件改为“ , ”,且 , 用含的式子表示的度数为 .23. 如图,已知数轴上A,B两点对应的数分别为 , 3.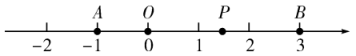 (1)、已知点P为数轴上一动点,其对应的数为x,若点P到点A,B的距离相等,则x=;(2)、若将数轴折叠,使与3表示的点重合.
(1)、已知点P为数轴上一动点,其对应的数为x,若点P到点A,B的距离相等,则x=;(2)、若将数轴折叠,使与3表示的点重合.①设与-3表示的点重合的点为数y,求y的值;
②若数轴上M,N两点之间的距离为2022,M在点N的左侧,且M,N两点经过折叠后互相重合,求M,N两点分别表示的数.