广东省茂名市茂南区2022-2023学年七年级上学期期末考试数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 实数﹣2023的绝对值是（）

A、2023 B、﹣2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 如图是由棱长均为1的小正方体组成的几何体，则这个几何体有____个小正方体，这个几何体的主视图的面积为____，以下选项正确的是（）．

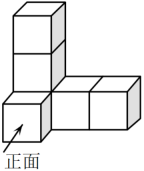A、5，5 B、5，4 C、6，5 D、6，4

查看试题解析
3. 下列计算结果是负数的是（）．

A、 $- (- \frac{1}{2})$ B、 $| - 2022 |$ C、 ${(- 2)}^{2}$ D、 ${(- 1)}^{3}$

查看试题解析
4. 下列问题中，最适合采用全面调查（普查）方式的是（）

A、调查一批灯泡的使用寿命 B、调查一架“歼20”飞机各零部件的质量 C、调查全国中学生对“天宫课堂”的了解情况 D、调查重庆市空气质量情况

查看试题解析
5. 如图，将一个无盖正方体展开成平面图形的过程中，需要剪开____条棱．

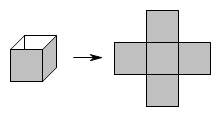A、3 B、4 C、5 D、不确定

查看试题解析
6. 如果一个多边形从一个顶点出发最多能画三条对角线，则这个多边形的边数为（）．

A、4 B、5 C、6 D、7

查看试题解析
7. 若 $4 a - 6 b = - 10$ ，则代数式5+2a-3b的值为（）．

A、0 B、-5 C、10 D、无法确定

查看试题解析
8. 方程 $2 x = \frac{1}{3} - \frac{4 x + 1}{6}$ 去分母后，正确的是（）．

A、 $2 x = 2 - (4 x + 1)$ B、 $12 x = 2 - 4 x + 1$ C、 $2 x = \frac{1}{3} - (4 x - 1)$ D、 $12 x = 2 - 4 x - 1$

查看试题解析
9. 下列各式中，正确的是（）．

A、 $a^{2} + a^{3} = a^{5}$ B、 $3 a \cdot a = 4 a$ C、 $8 x y - 6 x y = 2 x y$ D、 $2 x y^{2} - 2 x^{2} y = 0$

查看试题解析
10. 桌面上有甲､乙､丙三个圆柱形的杯子，杯深均为 $15 c m$ ，各装有 $10 c m$ 高的水，且表记录了甲､乙､丙三个杯子的底面积．今小明将甲､乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲､乙､丙三杯内水的高度比变为 $3 ： 4 ： 5$ ．若不计杯子厚度，则甲杯内水的高度变为（）

底面积（ $c m^{3}$ ）
甲杯
60
乙杯
80
丙杯
100

A、 $5.4 c m$ B、 $5.7 c m$ C、 $7.2 c m$ D、 $7.5 c m$

查看试题解析

二、填空题

11. 节约是一种传统美德，据不完全统计，全国每年浪费粮食总量折合粮食可养活约4040000000人，用科学记数法表示 $4.04 \times 1 0^{n}$ ，则n的值为．

查看试题解析
12. 截一个几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．如图，截面平行于底面，则这个几何体的截面是．

查看试题解析
13. 为了了解某地区初一年级 $5000$ 名学生的体重情况，从中抽取了 $480$ 名学生的体重，这个问题中的样本容量是．

查看试题解析
14. 如图，某养鸡户利用 $40 m$ 长的篱笆围建一个长方形鸡棚 $A B C D$ ，鸡棚的一边靠墙（墙足够长），在与墙平行的一边开一个 $2 m$ 宽的门．若设 $A D = x m$ ，则 $D C$ 的长表示为m．

查看试题解析
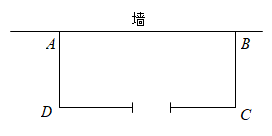15. 如图1，射线 $O C$ 在 $∠ A O B$ 的内部，图中共有3个角： $∠ A O B$ ， $∠ A O C$ 和 $∠ B O C$ ，若其中有一个角的度数是另一个角度数的两倍，则称射线 $O C$ 是 $∠ A O B$ 的“巧分线”，如图2，若 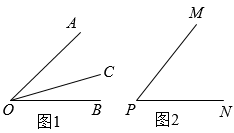$∠ M P N = 60 °$ ，且射线 $P Q$ 是 $∠ M P N$ 的“巧分线”，则 $∠ M P Q =$ ．

查看试题解析

三、解答题

16. 计算：

(1)、 $- 12 + 6 - (- 8)$ ；

(2)、 $6 \div (- \frac{3}{2}) + 1^{2022} - 2^{3}$ ．

查看试题解析
17.

(1)、化简： $- 3 a^{3} + 5 a - a^{3} + a$ ；

(2)、解方程： $\frac{1}{2} (3 x - 4) = \frac{1}{2} x - 2$ ．

查看试题解析
18. 某学校计划在七年级开设“折扇”“刺绣”“剪纸”“陶艺”四门校本课程，要求人人参加，并且只能选择其中一门课程，为了解学生对这四门课程的选择情况，学校从七年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图所示的条形统计图和扇形统计图．（部分信息未给出）
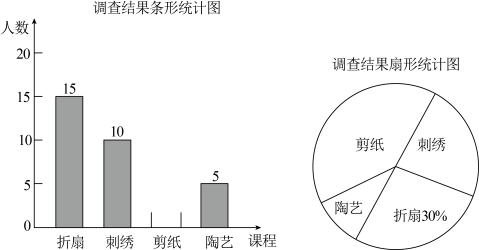
请你根据以上信息解决下列问题：

(1)、参加问卷调查的学生人数为 ▲ 名，补全条形统计图（画图并标注相应数据）；

(2)、“陶艺”课程所对应的扇形圆心角的度数是多少？

(3)、若该校七年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？

查看试题解析
19. 如图，已知线段 $A B$ ．

(1)、尺规作图：延长线段 $A B$ 到点C，使 $B C = 2 A B$ ；

(2)、在（1）的基础上，设D是 $A B$ 的中点， $A B$ 长为2，求 $D C$ 长；

(3)、在（1）的基础上，设D是 $A B$ 的中点， $A B$ 长为a，则 $D C =$ ．

查看试题解析
20. 已知： $A = 2 a^{2} + 3 a b - 1$ ， $B = a^{2} + a b + 1$ ．

(1)、求 $A - 2 B$ 的值；

(2)、若 ${(a - 1)}^{2000} + | b + 2 | = 0$ ，求（1）中 $A - 2 B$ 的值．

查看试题解析
21. 如图，利用黑白两种颜色的正六边形组成的图案，根据图案组成的规律回答下列问题：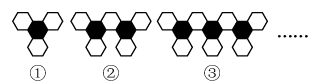

(1)、图案④中黑色六边形有个，白色六边形有个；

(2)、图案 $n$ 中黑色六边形有个，白色六边形有个；（用含 $n$ 的式子表示）

(3)、图案 $n$ 中的黑色六边形与白色六边形的和可能为2023个吗？若可能，请求出 $n$ 的值；若不可能，请说明理由．

查看试题解析
22. 某校准备购买篮球50个，跳绳 $x$ 条 $(x > 50)$ ．篮球定价80元/个，跳绳定价20元/条．商店甲、乙向学校提供了各自的优惠方案：
商店甲：买一个篮球送一条跳绳；
商店乙：篮球和跳绳都按定价的 $90 %$ 付款．

(1)、若该校到商店甲、乙购买，分别需付款多少元；（用含 $x$ 的代数式表示）

(2)、若 $x = 300$ ，通过计算说明此时哪间商店购买较为合算？

(3)、当 $x = 300$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并把付款的钱算出来．

查看试题解析
23. 如图数轴上有两个点A、B，分别表示的数是-2，4.请回答以下问题：

(1)、-2的绝对值是， A与B之间距离为；

(2)、若数轴上有点C，使得 $B C$ 的距离为3个单位长度，则点C表示的数是；

(3)、若点P从A点出发，以每秒5个单位长度的速度向右作匀速运动，点Q从B出发，以每秒3个单位长度的速度向右作匀速运动，P，Q同时运动，设运动的时间为t秒：
①当点P运动多少秒时，点P和点Q重合？
②当点P运动多少秒时，P，Q之间的距离为3个单位长度？

查看试题解析

	底面积（ $c m^{3}$ ）
甲杯	60
乙杯	80
丙杯	100