山西省晋中市平遥县2022-2023学年九年级上学期期末数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知x=1是方程x2+m=0的一个根,则m的值是( )A、﹣1 B、1 C、﹣2 D、23. 如果 ,那么 的值是( )A、 B、 C、 D、4. 如图,路灯距离地面8米,若身高1.6米的小明在路灯下处测得影子的长为5米,则小明和路灯的距离为( )
2. 已知x=1是方程x2+m=0的一个根,则m的值是( )A、﹣1 B、1 C、﹣2 D、23. 如果 ,那么 的值是( )A、 B、 C、 D、4. 如图,路灯距离地面8米,若身高1.6米的小明在路灯下处测得影子的长为5米,则小明和路灯的距离为( ) A、25米 B、15米 C、16米 D、20米5. “成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”描述的事件是不可能事件的是( )A、① B、② C、③ D、④6. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )
A、25米 B、15米 C、16米 D、20米5. “成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”描述的事件是不可能事件的是( )A、① B、② C、③ D、④6. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )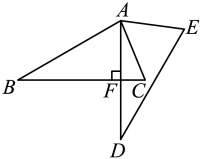 A、 B、 C、 D、7. 如图所示, , 是函数的图象上关于原点的任意一对对称点,平行于轴,平行于轴,的面积为 , 则( )
A、 B、 C、 D、7. 如图所示, , 是函数的图象上关于原点的任意一对对称点,平行于轴,平行于轴,的面积为 , 则( ) A、 B、 C、 D、8. 2020年,新型冠状病毒感染的肺炎疫情牵动着全国人民的心.某学生写了一份预防新型冠状病毒倡议书在微信朋友圈传播,规则为:将倡议书发表在自己的朋友圈,再邀请 个好友转发倡议书,每个好友转发倡议书,又邀请 个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有931人参与了传播活动,则方程列为( )A、 B、 C、 D、9. 如图,在矩形中,点的坐标是 , 则的长是( )
A、 B、 C、 D、8. 2020年,新型冠状病毒感染的肺炎疫情牵动着全国人民的心.某学生写了一份预防新型冠状病毒倡议书在微信朋友圈传播,规则为:将倡议书发表在自己的朋友圈,再邀请 个好友转发倡议书,每个好友转发倡议书,又邀请 个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有931人参与了传播活动,则方程列为( )A、 B、 C、 D、9. 如图,在矩形中,点的坐标是 , 则的长是( ) A、 B、8 C、 D、10. 如图,的三个顶点的坐标分别为 , , , 将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( )
A、 B、8 C、 D、10. 如图,的三个顶点的坐标分别为 , , , 将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 请写出一个三视图相同的几何体:.12. 一元二次方程的一般形式是 .13. 平行四边形的对角线与相交于点 , 若要使平行四边形成为矩形,则需要添加的一个条件是 . (只写出一种情况即可)14. 一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球试验,将球搅匀后任意摸出一个球,记下颜色后放回、搅匀,通过多次重复试验,算得摸到红球的频率是20%,则袋中有白球个数是 .15. 一块直角三角板 , , , , 测得边的中心投影长为 , 则长为cm.
 16. 如图,四边形的顶点都在坐标轴上,若 , 与面积分别为12和27,若双曲线恰好经过的中点 , 则的值为 .
16. 如图,四边形的顶点都在坐标轴上,若 , 与面积分别为12和27,若双曲线恰好经过的中点 , 则的值为 .
三、解答题
-
17.(1)、(2)、(3)、18. 如图,已知平行四边形中,延长至点 , 使 , 连接和 .
 (1)、求证:(2)、请你给图中补充适当的条件,使四边形成为菱形;请结合补充条件证明;19. 在抗击新冠病毒战役中,我县涌现出许多青年志愿者.其中小丽、小王等五名青年志愿者派往一社区核酸检测点,根据医护人员人事安排需要先抽出一人进行检测点消杀,再派两人到站点扫码,请你利用所学知识完成下列问题.(1)、小丽被派往检测点消杀的概率是;(2)、若正好抽出小丽小王之外的一人去往检测点消杀,剩下四人中再派两人去站点扫码,请你利用所学知识求出小丽和小王同时被派往站点扫码的概率.20. 已知反比例函数的图象与一次函数的图象交于点和点 .
(1)、求证:(2)、请你给图中补充适当的条件,使四边形成为菱形;请结合补充条件证明;19. 在抗击新冠病毒战役中,我县涌现出许多青年志愿者.其中小丽、小王等五名青年志愿者派往一社区核酸检测点,根据医护人员人事安排需要先抽出一人进行检测点消杀,再派两人到站点扫码,请你利用所学知识完成下列问题.(1)、小丽被派往检测点消杀的概率是;(2)、若正好抽出小丽小王之外的一人去往检测点消杀,剩下四人中再派两人去站点扫码,请你利用所学知识求出小丽和小王同时被派往站点扫码的概率.20. 已知反比例函数的图象与一次函数的图象交于点和点 . (1)、求这两个函数的关系式;(2)、观察图象,直接写出使得成立的自变量的取值范围;(3)、如果点与点关于轴对称,求的面积.21. 某商店通过网络在一源头厂家进一种季节性小家电,由于疫情影响以及市场竞争,该厂家不得不逐年下调出厂价;(1)、2019年这个小家电出厂价是每台62.5元,到2021年同期该品牌小家电出厂价下调为40元,若每年下调幅度相同,请你计算该小家电出厂价平均每年下调的百分率;(2)、若明年商场计划按每台40元购一批该品牌小家电,经市场预测,销售定价为50元时,每月可售出500台,销售定价每增加1元,销售量将减少10台.因受库存的影响,每月进货台数不得超过300台;商家若希望月获利8750元,则应进货多少台?销售定价多少元?22. 如图,正方形的边长是3,点是直线上一点,连接 , 将线段 , 将线段绕点逆时针旋转90°得到线段 , 在直线上取点 , 使 , 且点与点在同侧,连接 , .
(1)、求这两个函数的关系式;(2)、观察图象,直接写出使得成立的自变量的取值范围;(3)、如果点与点关于轴对称,求的面积.21. 某商店通过网络在一源头厂家进一种季节性小家电,由于疫情影响以及市场竞争,该厂家不得不逐年下调出厂价;(1)、2019年这个小家电出厂价是每台62.5元,到2021年同期该品牌小家电出厂价下调为40元,若每年下调幅度相同,请你计算该小家电出厂价平均每年下调的百分率;(2)、若明年商场计划按每台40元购一批该品牌小家电,经市场预测,销售定价为50元时,每月可售出500台,销售定价每增加1元,销售量将减少10台.因受库存的影响,每月进货台数不得超过300台;商家若希望月获利8750元,则应进货多少台?销售定价多少元?22. 如图,正方形的边长是3,点是直线上一点,连接 , 将线段 , 将线段绕点逆时针旋转90°得到线段 , 在直线上取点 , 使 , 且点与点在同侧,连接 , . (1)、如图①,当点在延长线上时,求证:四边形是平行四边形;(2)、如图②,当点在线段上时,四边形是否还是平行四边形,说明理由;(3)、在图②的条件下,四边形的面积是否存在正好等于正方形的面积的一半,若存在求出此时长;若不存在,请说明理由
(1)、如图①,当点在延长线上时,求证:四边形是平行四边形;(2)、如图②,当点在线段上时,四边形是否还是平行四边形,说明理由;(3)、在图②的条件下,四边形的面积是否存在正好等于正方形的面积的一半,若存在求出此时长;若不存在,请说明理由