山东省济南市高新区2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
2. $t a n 30 °$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
3. 下列各点中，在函数y=- $\frac{6}{x}$ 图象上的是（）

A、 $(- 2, - 4)$ B、 $(2, 3)$ C、 $(- 1, 6)$ D、 $(- \frac{1}{2}, 3)$

查看试题解析
4. 二次函数 $y = x^{2} - 6 x - 1$ 的二次项系数、一次项系数和常数项分别是（）

A、1， $- 6$ ， -1 B、1，6，1 C、0，-6，1 D、0，6，-1

查看试题解析
5. 如图，图形甲与图形乙是位似图形，点O是位似中心，点A、B的对应点分别为点 $A^{^{'}} 、 B^{^{'}}$ ，若 $O A^{'} = 2 O A$ ，则图形乙的面积是图形甲的面积的（）

A、2倍 B、3倍 C、4倍 D、5倍

查看试题解析
6. 如图所示，在房子的屋檐 $E$ 处安有一台监视器，房子前有一面落地的广告牌，那么监视器的盲区（）

A、△ACE B、△ADF C、△ABD D、四边形BCED

查看试题解析
7. 如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m 远，该同学的身高为1.7m ，则树高为（）.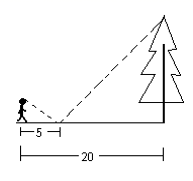

A、3.4m B、4.7 m C、5.1m D、6.8m

查看试题解析
8. 如图，两个反比例函数 $y = \frac{4}{x}$ 和 $y = \frac{2}{x}$ 在第一象限的图象分别是 $C_{1}$ 和 $C_{2}$ ，设点P在 $C_{1}$ 上， $P A ⊥ x$ 轴于点 $A$ ，交 $C_{2}$ 于 $B$ ，则 $△ P O B$ 的面积为（）

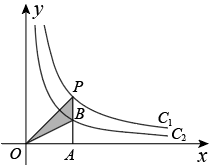A、1 B、2 C、3 D、4

查看试题解析
9. 如图，我市在建高铁的某段路基横断面为梯形 $A B C D$ ， $D C ∥ A B$ ． $B C$ 长6米，坡度为 $1 ： 1$ ， $A D$ 的坡度为 $1 ： \sqrt{3}$ ，则 $A D$ 长为（）米

A、 $6 \sqrt{2}$ B、 $8 \sqrt{2}$ C、 $6 \sqrt{3}$ D、 $8 \sqrt{3}$

查看试题解析
10. 若抛物线 $y = (x - m) (x - m - 3)$ 经过四个象限，则 $m$ 的取值范围是（）

A、 $m < - 3$ B、 $- 1 < m < 2$ C、 $- 3 < m < 0$ D、 $- 2 < m < 1$

查看试题解析

二、填空题

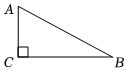
11. 如图，Rt△ABC中， $∠ C = 90 °$ ， AC＝5，BC＝12，则cosA的值为．

查看试题解析
12. 如图，是用若干个边长为1的小正方体堆积而成的几何体，该几何体的左视图的面积为。

查看试题解析
13. 已知反比例函数 $y = \frac{2 a - 3}{x}$ 的图象在每个象限内都是y随x的增大而增大，则a的取值范围为．

查看试题解析
14. 如图，已知点D、E在 $△ A B C$ 的边 $A B$ 和 $A C$ 上， $D E ∥ B C$ ， $A D = 10$ ， $B D = 5$ ， $A E = 6$ ，则 $A C =$ ．

查看试题解析
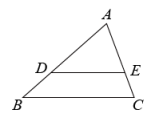15. 小聪在画一个二次函数的图象时，列出了下面几组y与x的对应值：
x
…
0
1
2
3
4
5
…
y
…
5
0
-3
-4
-3
0
…
该二次函数的解析式是．

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中，点E在边 $B C$ 上，连接 $A E$ 并延长，交对角线 $B D$ 于点F、 $D C$ 的延长线于点G．如果 $\frac{C E}{B E} = \frac{2}{3}$ ，则 $\frac{F E}{E G} =$

查看试题解析

三、解答题

17. 计算： $s i n 30 ° - t a n 30 ° \cdot t a n 60 ° + c o s^{2} 45 °$ ．

查看试题解析
18. 已知二次函数 $y = m x^{2} + (m - 1) x + m - 1$ 有最小值为0，求m的值．

查看试题解析
19. 如图：点D在△ABC的边AB上，连接CD，∠1＝∠B，AD＝4，AC＝6，求AB的长．

查看试题解析
20. 如图，某野外生态考察小组早晨7点整从A营地出发，准备前往正东方向的B营地，由于一条南北向河流的阻挡（图中阴影部分），他们需要从C处过桥．经过测量得知，A、B之间的距离为13 km，∠A和∠B的度数分别是37°和53°，桥CD的长度是0.5 km，图中的区域CDFE近似看做一个矩形区域．

(1)、求CE的长；

(2)、该考察小组希望到达B营地的时间不迟于中午12点，则他们的行进速度至少是多少？（结果保留1位小数）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
21. 如图，有一座抛物线形拱桥，在正常水位时桥下水面 $A B$ 的宽度为 $20 m$ ，这时拱高（点O到 $A B$ 的距离）为 $4 m$ ．

(1)、你能求出在图（a）的坐标系中，抛物线的函数表达式吗？

(2)、如果将直角坐标系建成如图（b）所示，抛物线的形状、表达式有变化吗？

查看试题解析
22. 如图1，长、宽均为3cm，高为8cm的长方体容器，放置在水平桌面上，里面盛有水，水面高为6cm，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，将这个情景转化成几何图形，如图3所示．

(1)、利用图1、图2所示水的体积相等，求 $D E$ 的长；

(2)、求水面高度 $C F$ ．

查看试题解析
23. 如图，点F是平行四边形 $A B C D$ 的边 $A D$ 上的一点，直线 $C F$ 交线段 $B A$ 的延长线于点E．

(1)、求证： $△ A E F ∽ △ D C F$ ；

(2)、若 $A F ： D F = 1 ： 2$ ， $A E = \sqrt{2}$ ， $S_{△ A E F} = \frac{2}{3}$
①求 $A B$ 的长；
②求 $△ E B C$ 的面积．

查看试题解析
24. 如图，直线 $y = k_{1} x + b$ 与双曲线 $y = \frac{k_{2}}{x}$ 交于A，B两点，已知点A的横坐标为 $- 3$ ，点B的纵坐标为 $- 3$ ，直线 $A B$ 与x轴交于点C，与y轴交于点 $D (0 ， - 2) ， t a n ∠ A O C = \frac{1}{3}$ ．

(1)、求双曲线和直线 $A B$ 的解析式；

(2)、若点P是第二象限内反比例函数图象上的一点， $△ O C P$ 的面积是 $△ O D B$ 的面积的3倍，求点P的坐标．

(3)、若点E在x轴的负半轴上，是否存在以点E，C，D为顶点构成的三角形与 $△ O D B$ 相似？若存在，求出点E的坐标；若不存在，请说明理由．

查看试题解析
25. 在数学兴趣小组活动中，同学们进行了以下数学探究活动．

(1)、【特例初探】
如图①， $A D$ 为 $△ A B C$ 的角平分线， $∠ A D B = 60 °$ ，点E在 $A C$ 上， $A E = A B$ ．求证： $D E$ 平分 $∠ A D C$ ．

(2)、如图②，在（1）的条件下，在 $A C$ 上取一点F，使 $B F = C F$ ， $B F$ 交 $A D$ 于点G．若 $B C = 10$ ， $D E = 4$ ，求 $D G$ 的长．

(3)、如图③，在四边形 $A B C D$ 中，对角线 $A C$ 平分 $∠ B A D$ ， $∠ A C D = 2 ∠ A C B$ ，点E是 $A C$ 上一点， $∠ E B C = ∠ A D C$ ．若 $B C = 2 \sqrt{5}$ ， $C D = 5$ ， $A B = \sqrt{2} A E$ ，求 $A C$ 的长．

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与x轴交于点 $A (- 1 ， 0) ， B (3 ， 0)$ ，与y轴交于点C，连接 $B C$ ．

(1)、求抛物线的函数表达式；

(2)、点 $D (m ， 0)$ 为线段OB上一动点（不与O，B重合），过点D作平行于y轴的直线交BC于点M，交抛物线于点N，是否存在点D使点M为线段DN的三等分点，若存在求出点D坐标，若不存在请说明理由；

(3)、过点O作直线 $l ∥ B C$ ，点P，Q为第一象限内的点，且Q在直线l上，P为l上方抛物线上的点，是否存在这样的点P，Q，使 $△ P Q B ∽ △ C O B$ ，若存在直接写出P，Q坐标，若不存在请说明理由．

查看试题解析

x	…	0	1	2	3	4	5	…
y	…	5	0	-3	-4	-3	0	…