吉林省长春市长春汽车经济技术开发区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 若函数是二次函数,则有( )A、 B、 C、 D、2. 下列命题是真命题的是( )A、直径是圆中最长的弦 B、三个点确定一个圆 C、平分弦的直径垂直于弦 D、相等的圆心角所对的弦相等3. 已知一元二次方程 , 下列判断正确的是( )A、该方程有两个相等的实数根 B、该方程有两个不相等的实数根 C、该方程无实数根 D、该方程根的情况无法确定4. 如图,在中,点 , 分别在 , 上,若 , 且的面积为4,则四边形的面积为( )
 A、5 B、8 C、9 D、125. 如图,木杆斜靠在墙壁上,是的中点,当木杆的上端沿墙壁竖直下滑时,木杆的底端也随之沿着射线方向滑动,则下滑过程中的长度变化情况是( )
A、5 B、8 C、9 D、125. 如图,木杆斜靠在墙壁上,是的中点,当木杆的上端沿墙壁竖直下滑时,木杆的底端也随之沿着射线方向滑动,则下滑过程中的长度变化情况是( ) A、逐渐变大 B、不断变小 C、不变 D、先变大再变小6. 在中, , , , 则的( )A、3 B、4 C、6 D、87. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为( )
A、逐渐变大 B、不断变小 C、不变 D、先变大再变小6. 在中, , , , 则的( )A、3 B、4 C、6 D、87. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为( )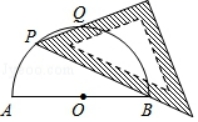 A、 B、 C、 D、18. 如图,已知点 , , 射线绕点逆时针旋转 , 与轴交于点 , 则过 , , 三点的二次函数中的值为( )
A、 B、 C、 D、18. 如图,已知点 , , 射线绕点逆时针旋转 , 与轴交于点 , 则过 , , 三点的二次函数中的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知二次函数y= x2的图象如图所示,线段AB∥x轴,交抛物线于A、B两点,且点A的横坐标为2,则AB的长度为 .
 10. 如图,在中, , , 以为直径的交于点 . 是上一点,且 , 连接 . 过点作 , 交的延长线于点 , 则为 .
10. 如图,在中, , , 以为直径的交于点 . 是上一点,且 , 连接 . 过点作 , 交的延长线于点 , 则为 . 11. 随着国内新冠疫情逐步得到控制,人们的口罩储备逐渐充足,市场的口罩需求量在逐渐减少,某口罩厂六月份的口罩产量为100万只,由于市场需求量减少,八月份的产量减少到81万只,则该厂七八月份的口罩产量的月平均减少率为12. 如图,与位似,点O为位似中心,位似比为 . 若的周长为6,则的周长是 .
11. 随着国内新冠疫情逐步得到控制,人们的口罩储备逐渐充足,市场的口罩需求量在逐渐减少,某口罩厂六月份的口罩产量为100万只,由于市场需求量减少,八月份的产量减少到81万只,则该厂七八月份的口罩产量的月平均减少率为12. 如图,与位似,点O为位似中心,位似比为 . 若的周长为6,则的周长是 .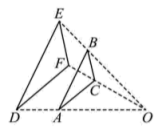 13. 三个正方形方格和扇形的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形的面积为 .
13. 三个正方形方格和扇形的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形的面积为 . 14. 已知点与点的坐标,抛物线与线段有交点,则的取值范围是 .
14. 已知点与点的坐标,抛物线与线段有交点,则的取值范围是 .三、解答题
-
15. 解方程16. 如图,AB是 的直径,弦 于点E,若 , ,求 的长.
 17. 图①、图②均是由边长为1的小正方形组成的5×5的网格,每个小正方形的顶点称为格点,的顶点均在格点上,在图①、图②给定的网格中,只用无刻度直尺,保留作图痕迹,按要求作图:
17. 图①、图②均是由边长为1的小正方形组成的5×5的网格,每个小正方形的顶点称为格点,的顶点均在格点上,在图①、图②给定的网格中,只用无刻度直尺,保留作图痕迹,按要求作图: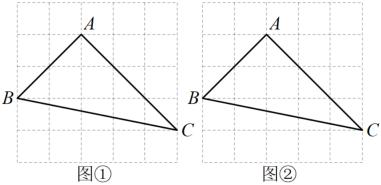 (1)、图①中,的长为 .(2)、在图①中的BC边上确定一点P,使点P到三个顶点距离相等.(3)、在图②中,在的边上确定一点M,使得 .18. 在平面直角坐标系中,抛物线经过点、(1)、这条抛物线所对应的函数表达式 .(2)、这条抛物线与轴的交点坐标 .(3)、当时,的取值范围为 .19. 如图,为的直径,为上一点,的平分线交于点 , 于点 .
(1)、图①中,的长为 .(2)、在图①中的BC边上确定一点P,使点P到三个顶点距离相等.(3)、在图②中,在的边上确定一点M,使得 .18. 在平面直角坐标系中,抛物线经过点、(1)、这条抛物线所对应的函数表达式 .(2)、这条抛物线与轴的交点坐标 .(3)、当时,的取值范围为 .19. 如图,为的直径,为上一点,的平分线交于点 , 于点 . (1)、求证:为的切线;(2)、若 , , 则弧的长为 .20. 近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图(台灯底座高度忽略不计)如图2所示,其中灯柱 , 灯臂 , 灯罩 , , CD、DE分别可以绕点C、D上下调节一定的角度.经使用发现:当 , 且时,台灯光线最佳.求此时点D到桌面AB的距离.(精确到0.1cm,参考数值: , , )
(1)、求证:为的切线;(2)、若 , , 则弧的长为 .20. 近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图(台灯底座高度忽略不计)如图2所示,其中灯柱 , 灯臂 , 灯罩 , , CD、DE分别可以绕点C、D上下调节一定的角度.经使用发现:当 , 且时,台灯光线最佳.求此时点D到桌面AB的距离.(精确到0.1cm,参考数值: , , ) 21. 某商店购进了一种消毒用品,进价为每件9元,在销售过程中发现,每天的销售量(件)与每件售价(元)之间存在一次函数关系(其中 , 且为整数).设该商店销售这种消毒用品每天获利(元).(1)、求与之间的函数关系式;(2)、当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?22. 在一次数学探究活动中,王老师设计了一份活动单:
21. 某商店购进了一种消毒用品,进价为每件9元,在销售过程中发现,每天的销售量(件)与每件售价(元)之间存在一次函数关系(其中 , 且为整数).设该商店销售这种消毒用品每天获利(元).(1)、求与之间的函数关系式;(2)、当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?22. 在一次数学探究活动中,王老师设计了一份活动单:已知线段 , 使用作图工具作 .
尝试操作后思考:这样的点唯一吗?点的位置有什么特征?你有什么感悟?
“神州”学习小组通过操作、观察、讨论后汇报:点的位置不唯一,它在以为弦的圆弧上(点、除外),…小乐同学画出了符合要求的一条圆弧(如图1).
 (1)、小乐同学提出了下列问题,请你帮助解决.
(1)、小乐同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为;
②面积的最大值为;
(2)、经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形外部,我们记为 , 请你利用图1证明 .(3)、请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形的边长 , , 点在直线的右侧,且 , 则线段长的最大值为 .23. 如图,在中, , , , 动点从点出发,沿以每秒2个单位长度的速度向终点匀速运动,设点的运动时间为秒 . 过点作的垂线交于点 . (1)、AC= .(2)、求的长.(用含有的代数式表示)(3)、若将点绕点逆时针旋转于点 .
(1)、AC= .(2)、求的长.(用含有的代数式表示)(3)、若将点绕点逆时针旋转于点 .①求的长(用含的代数式表示)
②在点运动的同时,做点关于点的对称点 , 连结 , 当为等腰三角形时,直接写出的值.
24. 在平面直角坐标系中,已知抛物线顶点的坐标为 , 抛物线上不重合的两点、的横坐标分别为 , .(1)、b=(2)、若、两点的纵坐标相等,求m的值.(3)、当点在对称轴左侧时,将抛物线上、两点之间(含、两点)的图象记为 , 设图象的最高点与最低点的纵坐标之差为 , 求与之间的函数关系式.(4)、当点在点的右侧时,过、两点分别向抛物线的对称轴作垂线,垂足分别为点、 . 若点、、中任意两点不重合且其中一点到另两点距离相等,直接写出的值.