吉林省长春市榆树市2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 当函数 $y = (a - 1) x^{2} + b x + c$ 是二次函数时，a的取值为（）

A、 $a = 1$ B、 $a = - 1$ C、 $a \neq - 1$ D、 $a \neq 1$

查看试题解析
2. 下列各组中的四条线段成比例的是（　　）

A、a=1，b=3，c=2，d=4 B、a=4，b=6，c=5，d=10 C、a=2，b=4，c=3，d=6 D、a=2，b=3，c=4，d=1

查看试题解析
3. 掷一枚均匀的正方体骰子，掷得“6”的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
4. 随着生产技术的进步，生产成本逐年下降．某工厂两年前生产一台扫地机器人的成本是900元，现在生产一台扫地机器人的成本是600元．设该种扫地机器人生产成本的年平均下降率为x，则下面所列方程正确的是（）

A、 $900 \times {(1 - x)}^{2} = 600$ B、 $900 \times 2 (1 - x) = 600$ C、 $900 \times (1 - 2 x) = 600$ D、 $900 \times (1 - x^{2}) = 600$

查看试题解析
5. 已知二次函数 $y = a x^{2} + b x + c$ 的图像开口向下，顶点坐标为 $(3 ， - 7)$ ，那么该二次函数有（）

A、最小值-7 B、最大值-7 C、最小值3 D、最大值3

查看试题解析
6. 如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开．若测得AB的长为10km，则M，C两点间的距离为（）

A、3km B、4km C、5km D、6km

查看试题解析
7. 如图，在坡角为 $α$ 的山坡上栽树，要求相邻两树之间的水平距离为6米，那么相邻两树在坡面上的距离AB为（）

A、 $6 c o s α$ B、 $\frac{6}{c o s α}$ C、 $6 s i n α$ D、 $\frac{6}{s i n α}$

查看试题解析
8. 如图，在Rt△ABC中， $∠ B A C = 90 °$ ， $A B = 6$ ， $A C = 8$ ，点P为BC上任意一点，连结PA，以PA、PC为邻边作 $▱$ PAQC，连结PQ，则PQ的最小值为（）

A、 $\frac{12}{5}$ B、3 C、 $\frac{24}{5}$ D、5

查看试题解析

二、填空题

9. 已知二次函数 $y = 3 x^{2}$ ，则其图像的开口向．（填“上”或“下”）

查看试题解析
10. 关于x的一元二次方程 $x^{2} - 3 x + k = 0$ 有两个相等的实数根，则k的值为．

查看试题解析
11. 下列事件：①长春市某天的最低气温为-200℃；②人们外出旅游时，使用手机App购买景点门票；③在平面内任意画一个三角形，其内角和等于180°，其中是随机事件的是（只填写序号）．

查看试题解析
12. 如图，在△ABC中， $C D ⊥ A B$ ，垂足为D．若 $A B = 12$ ， $C D = 6$ ， $t a n A = \frac{3}{2}$ ，则 $s i n B$ 的值为．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以顶点 $A$ 为圆心，适当长为半径画弧，分别交 $A B$ ， $A C$ 于点 $N$ ， $M$ ，再分别以点 $M N$ 为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点 $P$ ，射线交边 $C$ 于点 $D$ ，若 $△ D A C ∽ △ A B C$ ，则 $∠ B =$ 度．

查看试题解析
14. 如图，在平面直角坐标系中，抛物线y＝﹣ $\frac{2}{3}$ （x﹣3）²+k经过坐标原点O，与x轴的另一个交点为A．过抛物线的顶点B分别作BC⊥x轴于C、BD⊥y轴于D，则图中阴影部分图形的面积和为．

查看试题解析

三、解答题

15. 计算： $(\sqrt{24} - \sqrt{6})$ ÷ $\sqrt{3} + \sqrt{\frac{1}{2}}$

查看试题解析
16. 解方程： $3 x^{2} + 6 x - 4 = 0$ ．

查看试题解析
17. 小华有3张卡片，小明有2张卡片，卡片上的数字如图所示．小华和小明分别从自己的卡片中随机抽取一张．请用画树状图（或列表）的方法，求抽取的两张卡片上的数字和为6的概率．

查看试题解析
18. 已知关于x的一元二次方程mx²﹣（m+2）x+2=0．

(1)、证明：不论m为何值时，方程总有实数根；

(2)、m为何整数时，方程有两个不相等的正整数根．

查看试题解析
19. 如图，小莹在数学综合实践活动中，利用所学的数学知识对某小区居民楼AB的高度进行测量．先测得居民楼AB与CD之间的距离AC为35m，后站在M点处测得居民楼CD的顶端D的仰角为45°．居民楼AB的顶端B的仰角为55°．已知居民楼CD的高度为16.6m，小莹的观测点N距地面1.6m．求居民楼AB的高度（精确到1m）．（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）

查看试题解析
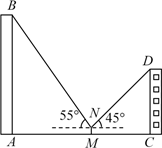20. 如图，边长为2的正方形 $O A B C$ 的顶点A，C分别在x轴，y轴的正半轴上，二次函数 $y = - x^{2} + b x + c$ 的图象经过B，C两点．

(1)、求b，c的值；

(2)、若将该抛物线向下平移m个单位，使其顶点落在正方形 $O A B C$ 内（不包括边上），求m的取值范围．

查看试题解析
21. 按要求作图（必须用直尺连线）：

(1)、在图①中以点C为位似中心，在网格中画出△DEC，使△DEC与△ABC位似，且△DEC与△ABC的位似比为2：1，

(2)、在图②中找到一个格点C，使∠ACB是锐角，且tan∠ACB＝1，并画出△ACB．

查看试题解析
22.

(1)、【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题，请完成这道题的证明．

(2)、【结论应用】
如图②，在上边题目的条件下，延长图①中的线段 $A D$ 的延长线交 $N M$ 的延长线于点E，延长线段 $B C$ 交 $N M$ 的延长线于点F．求证： $∠ A E N = ∠ F$ ．

(3)、若（1）中的 $∠ A + ∠ A B C = 122 °$ ，则 $∠ F$ 的大小为．

查看试题解析
23. 【阅读材料】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如 $3 + 2 \sqrt{2} = {(1 + \sqrt{2})}^{2}$ ．善于思考的小明进行了以下探索：若设 $a + b \sqrt{2} = {(m + n \sqrt{2})}^{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ （其中 $a 、 b 、 m 、 n$ 均为整数），则有 $a = m^{2} + 2 n^{2} ， b = 2 m n$ ．这样小明就找到了一种把类似 $a + b \sqrt{2}$ 的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：

(1)、【问题解决】
若 $a + b \sqrt{5} = {(m + n \sqrt{5})}^{2}$ ，当 $a 、 b 、 m 、 n$ 均为整数时，则a＝， b＝．（均用含m、n的式子表示）

(2)、若 $x + 4 \sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，且 $x 、 m 、 n$ 均为正整数，分别求出 $x 、 m 、 n$ 的值．

(3)、【拓展延伸】
化简 $\sqrt{5} + 2 \sqrt{6}$ ＝．

查看试题解析
24. 如图，在 $▱$ ABCD中， $A D = 10$ ， $A B = 8$ ， $B D ⊥ A B$ ．点P从点A出发，沿折线AB—BC以每秒2个单位长度的速度向终点C运动（点P不与点A、B、C重合）．在点P的运动过程中，过点P作AB所在直线的垂线，交边AD或边CD于点Q，以PQ为一边作矩形PQMN，且 $Q M = 4$ ， MN与BD在PQ的同侧．设点P的运动时间为t（秒）．

(1)、 $t a n A$ 的值为．

(2)、求线段PQ的长．（用含t的代数式表示）

(3)、当 $t = 6$ 时，求△PCQ的面积．

(4)、连接 AC．当点M或点N落在AC上时，直接写出t的值．

查看试题解析