广东省阳江市阳西县2022-2023学年九年级上学期期末考试数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件是必然事件的是( )A、三角形内角和是180° B、端午节赛龙舟,红队获得冠军 C、掷一枚均匀骰子,点数是6的一面朝上 D、打开电视,正在播放神舟十四号载人飞船发射实况3. 若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )A、﹣1 B、0 C、1 D、24. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
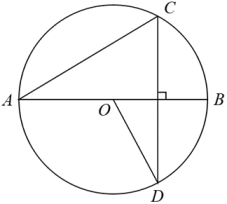
2. 下列事件是必然事件的是( )A、三角形内角和是180° B、端午节赛龙舟,红队获得冠军 C、掷一枚均匀骰子,点数是6的一面朝上 D、打开电视,正在播放神舟十四号载人飞船发射实况3. 若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )A、﹣1 B、0 C、1 D、24. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )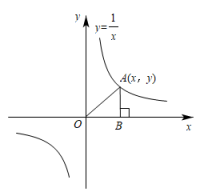 A、1 B、 C、2 D、5. 如图,四边形是的内接四边形,若 , 则的度数是( )
A、1 B、 C、2 D、5. 如图,四边形是的内接四边形,若 , 则的度数是( )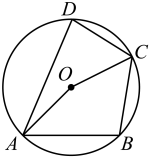 A、 B、 C、 D、6. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
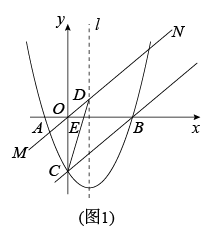
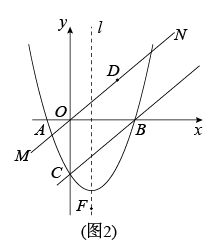
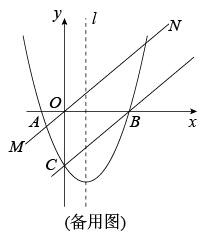
A、 B、 C、 D、6. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、8. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=509. 已知都在反比例函数的图像上,则、、的大小关系是( )A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )
A、 B、 C、 D、8. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=509. 已知都在反比例函数的图像上,则、、的大小关系是( )A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )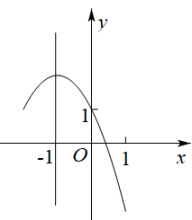 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .12. 若关于的一元二次方程有实数根,则实数k的取值范围是.13. 质检部门对某批产品的质量进行随机抽检,结果如下表所示:
抽检产品数n
100
150
200
250
300
500
1000
合格产品数m
89
134
179
226
271
451
904
合格率
0.890
0.893
0.895
0.904
0.903
0.902
0.904
在这批产品中任取一件,恰好是合格产品的概率约是(结果保留一位小数) .
14. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).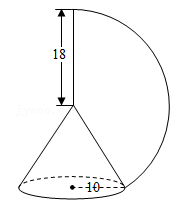 15. 如图, 中, 是 内部的一个动点,且满足 则线段 的最小值为 .
15. 如图, 中, 是 内部的一个动点,且满足 则线段 的最小值为 .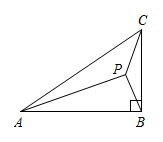
三、解答题
-
16. 解方程:17. 在如图所示的方格纸(1格长为一个单位长度)中,的三个顶点坐标分别为 , , .
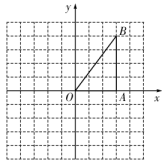 (1)、将绕点O顺时针旋转 , 画出旋转后的;(2)、在(1)的条件下,求点B绕点O旋转到点所经过的路径长(结果保留).18. 一只不透明的袋子中装有3个大小、质地完全相同的乒乓球,球面上分别标有数字1、2、3,搅匀后先从袋子中任意摸出1个球,记下数字后放回,搅匀后再从袋子中任意摸出1个球,记下数字.(1)、第一次摸到标有偶数的乒乓球的概率是;(2)、用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.19. 商店销售某种商品,经调查发现,平均每天销售40件,每件盈利20元,若每件降价1元,则每天可多销售10件.如果每天要盈利1080元,同时又要使顾客得到更多的实惠,每件应降价多少元?20. 如图,一次函数的图像与反比例函数的图像交于点 , 与y轴交于点B,与x轴交于点 .
(1)、将绕点O顺时针旋转 , 画出旋转后的;(2)、在(1)的条件下,求点B绕点O旋转到点所经过的路径长(结果保留).18. 一只不透明的袋子中装有3个大小、质地完全相同的乒乓球,球面上分别标有数字1、2、3,搅匀后先从袋子中任意摸出1个球,记下数字后放回,搅匀后再从袋子中任意摸出1个球,记下数字.(1)、第一次摸到标有偶数的乒乓球的概率是;(2)、用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.19. 商店销售某种商品,经调查发现,平均每天销售40件,每件盈利20元,若每件降价1元,则每天可多销售10件.如果每天要盈利1080元,同时又要使顾客得到更多的实惠,每件应降价多少元?20. 如图,一次函数的图像与反比例函数的图像交于点 , 与y轴交于点B,与x轴交于点 .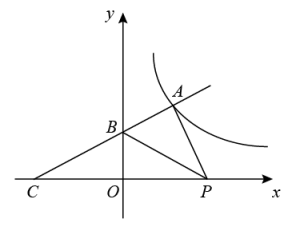 (1)、求k与m的值;(2)、为x轴上的一动点,当△APB的面积为时,求a的值.21. 为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x( , 且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求y关于x的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?
(1)、求k与m的值;(2)、为x轴上的一动点,当△APB的面积为时,求a的值.21. 为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x( , 且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求y关于x的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?