广东省广州市黄埔区2022-2023学年九年级上学期期末考试数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 下列关于防范“新冠肺炎”的标志中是中心对称图形的是( )A、戴口罩讲卫生
 B、勤洗手勤通风
B、勤洗手勤通风 C、有症状早就医
C、有症状早就医 D、少出门少聚集
D、少出门少聚集 2. “掷一枚质地均匀的骰子,向上一面点数为6”这个事件是( )A、随机事件 B、确定事件 C、不可能事件 D、必然事件3. 若关于的方程是一元二次方程,则的取值范围是( )A、 B、 C、 D、4. 抛物线的顶点坐标是( )A、 B、 C、 D、5. 如图,是的直径, , 是的切线,则的度数为( )
2. “掷一枚质地均匀的骰子,向上一面点数为6”这个事件是( )A、随机事件 B、确定事件 C、不可能事件 D、必然事件3. 若关于的方程是一元二次方程,则的取值范围是( )A、 B、 C、 D、4. 抛物线的顶点坐标是( )A、 B、 C、 D、5. 如图,是的直径, , 是的切线,则的度数为( ) A、 B、 C、 D、6. 已知反比例函数经过两点 , , 则( )A、 B、 C、 D、7. 如图,是某商店售卖的花架,其中 , , , , 则长为( )cm.
A、 B、 C、 D、6. 已知反比例函数经过两点 , , 则( )A、 B、 C、 D、7. 如图,是某商店售卖的花架,其中 , , , , 则长为( )cm. A、 B、 C、50 D、308. 关于的一元二次方程有两个不相等的实数根,则的值可能是( )A、2 B、3 C、4 D、59. 已知一次函数的图象如下图所示,则二次函数的图象大致位置是( )
A、 B、 C、50 D、308. 关于的一元二次方程有两个不相等的实数根,则的值可能是( )A、2 B、3 C、4 D、59. 已知一次函数的图象如下图所示,则二次函数的图象大致位置是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,将正六边形放置在直角坐标系内, , 点B在原点,点P是正六边形的中心,现把正六边形沿x轴正半轴作无滑动的连续翻转,每次翻转 , 经过2022次翻转之后,则点Р的坐标是( )
10. 如图,将正六边形放置在直角坐标系内, , 点B在原点,点P是正六边形的中心,现把正六边形沿x轴正半轴作无滑动的连续翻转,每次翻转 , 经过2022次翻转之后,则点Р的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知点与点关于原点对称,则点坐标为 .12. 若2是关于的方程的一个根,则 .13. 如图,以点О为位似中心,将缩小得到 , 若 , 的周长为2,则的周长为 .
 14. 如图,二次函数的图象过点且对称轴为直线 , 则关于的一元二次方程的解为 .
14. 如图,二次函数的图象过点且对称轴为直线 , 则关于的一元二次方程的解为 . 15. 如图,在直角三角形中, , , 将顺时针旋转得到 , 与相交于点 , 则的长为 . (结果保留根号)
15. 如图,在直角三角形中, , , 将顺时针旋转得到 , 与相交于点 , 则的长为 . (结果保留根号) 16. 定义:若一个矩形中,一组对边的两个三等分点在同一个反比例函数的图象上,则称这个矩形为“奇特矩形”.如图,在直角坐标系中,矩形是第一象限内的一个“奇特矩形”、且点 , , 则的长为 .
16. 定义:若一个矩形中,一组对边的两个三等分点在同一个反比例函数的图象上,则称这个矩形为“奇特矩形”.如图,在直角坐标系中,矩形是第一象限内的一个“奇特矩形”、且点 , , 则的长为 .
三、解答题
-
17. 解方程: .18. 如图,的直径 , 是的弦, , 垂足为M, , 求的长.
 19. 如图,已知 , , 垂足分别为B、C,交于点D, , , , 求的长.
19. 如图,已知 , , 垂足分别为B、C,交于点D, , , , 求的长. 20. 新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年出口量逐年增加,2020年出口量为20万台,2022年出口量增加到45万台.(1)、求2020年到2022年新能源汽车出口量的年平均增长率是多少?(2)、按照这个增长速度,预计2023年我国新能源汽车出口量为多少?21. 2022年3月23日“天宫课堂”第二课正式开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩.为此,我区某校组织九年级全体学生进行了“天宫课堂”知识竞赛,赛后对全体参赛选手的竞赛成绩进行了整理与统计,结果如下表:
20. 新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年出口量逐年增加,2020年出口量为20万台,2022年出口量增加到45万台.(1)、求2020年到2022年新能源汽车出口量的年平均增长率是多少?(2)、按照这个增长速度,预计2023年我国新能源汽车出口量为多少?21. 2022年3月23日“天宫课堂”第二课正式开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩.为此,我区某校组织九年级全体学生进行了“天宫课堂”知识竞赛,赛后对全体参赛选手的竞赛成绩进行了整理与统计,结果如下表:组别
分数段
频数(人)
频率
1
60分以下
30
0.1
2
45
0.15
3
60
4
0.4
5
45
0.15
请根据以上信息,解答下列问题:
(1)、表中m= , n=;(2)、竞赛结束后,九(1)班得分前4名的同学中,刚好有2名男同学和2名女同学,现准备从中选取两名同学宣讲“天宫课堂”知识,请用列举法求这两名同学恰好是一男一女的概率.22. 如图,的三个顶点的坐标分别为 , , , 将绕原点О逆时针旋转90°得到. (1)、请画出 , 并写出点的坐标.(2)、在旋转过程中,线段扫过的图形恰好是一个圆锥的侧面展开图,求这个圆锥的底面圆的半径.23. 如图,已知点A在反比例函数的图象上,点A的横坐标为 , 过点A作轴,垂足为B,且 .
(1)、请画出 , 并写出点的坐标.(2)、在旋转过程中,线段扫过的图形恰好是一个圆锥的侧面展开图,求这个圆锥的底面圆的半径.23. 如图,已知点A在反比例函数的图象上,点A的横坐标为 , 过点A作轴,垂足为B,且 . (1)、求该反比例函数的解析式;(2)、若点在x轴的正半轴上,将线段绕着点P顺时针旋转90°,点A的对应点C恰好落在反比例函数在第一象限的图象上,求m的值.24. 如图1,为的外接圆,半径为6, , , 点为优弧上异于的一动点,连接 .
(1)、求该反比例函数的解析式;(2)、若点在x轴的正半轴上,将线段绕着点P顺时针旋转90°,点A的对应点C恰好落在反比例函数在第一象限的图象上,求m的值.24. 如图1,为的外接圆,半径为6, , , 点为优弧上异于的一动点,连接 .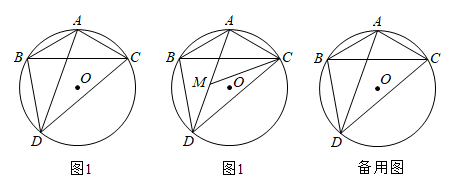 (1)、求证:平分;(2)、如图2,平分 , 且与交于 .
(1)、求证:平分;(2)、如图2,平分 , 且与交于 .花花同学认为:无论点运动到哪里,始终有;
都都同学认为:的长会随着点运动而变化.
你赞同谁的观点,请说明理由;
(3)、求的最大值.25. 已知抛物线(是常数)与x轴交于A,B两点,A在B的左侧.(1)、若抛物线的对称轴为直线 , 求抛物线的解析式;(2)、在(1)的条件下, , 是抛物线上的两点,点P是线段CD下方抛物线上的一动点,连接PC,PD,求的面积最大值;(3)、已知代数式 , 记抛物线位于轴下方的图象为 , 抛物线位于x轴上方的图象为 , 将沿轴翻折得图象 , 与组合成的新图象记为 , 当直线与图象T有两个交点时,结合图象求M的取值范围.