北京市西城区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 二次函数y=(x-2)2+3的最小值是( )A、3 B、2 C、-2 D、-32. 中国传统扇文化有着深厚的文化底蕴,是中华民族文化的一个组成部分,在中国传统社会中,扇面形状的设计与日常生活中的图案息息相关,下列扇面图形中,既是轴对称图形,又是中心对称图形的是( )
 A、
A、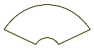 B、
B、 C、
C、 D、
D、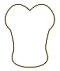 3. 下列事件中是随机事件的是( )A、明天太阳从东方升起 B、经过有交通信号灯的路口时遇到红灯 C、平面内不共线的三点确定一个圆 D、任意画一个三角形,其内角和是4. 如图,在中,弦 , 相交于点 , , , 则的大小是( )
3. 下列事件中是随机事件的是( )A、明天太阳从东方升起 B、经过有交通信号灯的路口时遇到红灯 C、平面内不共线的三点确定一个圆 D、任意画一个三角形,其内角和是4. 如图,在中,弦 , 相交于点 , , , 则的大小是( )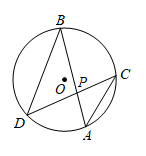 A、35° B、45° C、60° D、70°5. 抛物线通过变换可以得到抛物线 , 以下变换过程正确的是( )A、先向右平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向下平移2个单位 D、先向左平移1个单位,再向上平移2个单位6. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都只赛一场),计划安排15场比赛,如果设邀请个球队参加比赛,那么根据题意可以列方程为( )A、 B、 C、 D、7. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )
A、35° B、45° C、60° D、70°5. 抛物线通过变换可以得到抛物线 , 以下变换过程正确的是( )A、先向右平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向下平移2个单位 D、先向左平移1个单位,再向上平移2个单位6. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都只赛一场),计划安排15场比赛,如果设邀请个球队参加比赛,那么根据题意可以列方程为( )A、 B、 C、 D、7. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )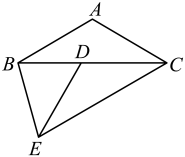 A、30° B、45° C、55° D、75°8. 下表记录了二次函数中两个变量与的5组对应值,其中 .
A、30° B、45° C、55° D、75°8. 下表记录了二次函数中两个变量与的5组对应值,其中 .…
-5
1
3
…
…
0
2
0
…
根据表中信息,当时,直线与该二次函数图象有两个公共点,则的取值范围是( )
A、 B、 C、 D、二、填空题
-
9. 一元二次方程x2﹣16=0的解是 .10. 已知的半径为5,点到圆心的距离为8,则点在(填“内”“上”或“外”).11. 若关于 的一元二次方程 有两个相等的实数根,则 的值为 .12. 圆心角是60°的扇形的半径为6,则这个扇形的面积是 .13. 点是抛物线上一点,则的值是 , 点关于原点对称的点的坐标是 .14. 已知二次函数满足条件:①图像象过原点;②当时,随的增大而增大,请你写出一个满足上述条件的二次函数的解析式: .15. 如图,在平面直角坐标系中,以点为圆心,1为半径画圆,将绕点逆时针旋转得到 , 使得与轴相切,则的度数是 .
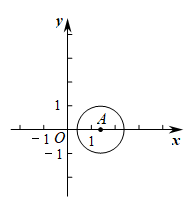 16. 如图,是的直径,为上一点,且 , 为圆上一动点,为的中点,连接 , 若的半径为2,则长的最大值是 .
16. 如图,是的直径,为上一点,且 , 为圆上一动点,为的中点,连接 , 若的半径为2,则长的最大值是 .
三、解答题
-
17. 解方程:18. 已知:点 , , 在上,且 .
求作:直线 , 使其过点 , 并与相切.
作法:①连接;
②分别以点 , 点为圆心,长为半径作弧,两弧交于外一点;
③作直线 .
直线就是所求作直线 .
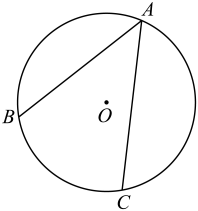 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 , ,
∵ ,
∴四边形是菱形,
∵点 , , 在上,且 ,
∴ ▲ °( )(填推理的依据).
∴四边形是正方形,
∴ , 即 ,
∵为半径,
∴直线为的切线( )(填推理的依据).
19. 已知二次函数 .(1)、将化成的形式,并写出它的顶点坐标;(2)、在所给的平面直角坐标系中画出此函数的图象;(3)、当时,结合图象,直接写出函数值的取值范围.20. 如图,是的一条弦,点是的中点,连接并延长交劣弧于点 , 连接 , , 若 , , 求的面积. 21. 在学习《用频率估计概率》时,小明和他的伙伴们设计了一个摸球试验:在一个不透明帆布袋中装有白球和红球共4个,这4个球除颜色外无其他差别,每次摸球前先将袋中的球搅匀,然后从袋中随机摸出1个球,观察该球的颜色并记录,再把它放回,在老师的帮助下,小明和他的伙伴们用计算机模拟这个摸球试验,下图显示的是这个试验中摸出一个球是红球的结果.
21. 在学习《用频率估计概率》时,小明和他的伙伴们设计了一个摸球试验:在一个不透明帆布袋中装有白球和红球共4个,这4个球除颜色外无其他差别,每次摸球前先将袋中的球搅匀,然后从袋中随机摸出1个球,观察该球的颜色并记录,再把它放回,在老师的帮助下,小明和他的伙伴们用计算机模拟这个摸球试验,下图显示的是这个试验中摸出一个球是红球的结果.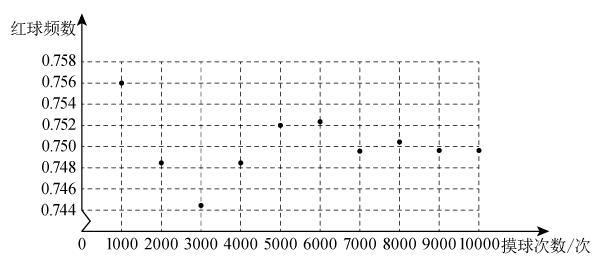 (1)、根据所学的频率与概率关系的知识,估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是 , 其中红球的个数是;(2)、如果从这个不透明的帆布袋中同时摸出两个球,用列举法求摸出的两个球刚好一个是红球和一个是白球的概率.22. 如图,在四边形中, , 是对角线,将点绕点逆时针旋转60°得到点 , 连接 , , .
(1)、根据所学的频率与概率关系的知识,估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是 , 其中红球的个数是;(2)、如果从这个不透明的帆布袋中同时摸出两个球,用列举法求摸出的两个球刚好一个是红球和一个是白球的概率.22. 如图,在四边形中, , 是对角线,将点绕点逆时针旋转60°得到点 , 连接 , , .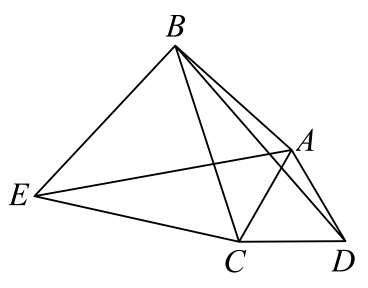 (1)、求的度数;(2)、若是等边三角形,且 , , , 求的长.23. 已知关于的方程 .(1)、求证:方程有两个不相等的实数根;(2)、设此方程的两个根分别为 , , 且 , 若 , 求的值.24. 如图,在中, , , 点是上一点,以为圆心,长为半径作圆,使与相切于点 , 与相交于点 . 过点作 , 交的延长线于点 .
(1)、求的度数;(2)、若是等边三角形,且 , , , 求的长.23. 已知关于的方程 .(1)、求证:方程有两个不相等的实数根;(2)、设此方程的两个根分别为 , , 且 , 若 , 求的值.24. 如图,在中, , , 点是上一点,以为圆心,长为半径作圆,使与相切于点 , 与相交于点 . 过点作 , 交的延长线于点 .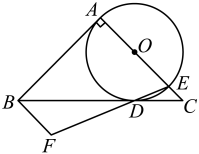 (1)、若 , 求的半径;(2)、连接 , 求证:四边形是平行四边形.25. 跳台滑雪是冬季奥运会的比赛项目之一,如图,运动员通过助滑道后在点处起跳经空中飞行后落在着陆坡上的点处,他在空中飞行的路线可以看作抛物线的一部分,这里表示起跳点到地面的距离,表示着陆坡的高度,表示着陆坡底端到点的水平距离,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度(单位:m)与水平距离(单位:m)近似满足函数关系: , 已知 , , 落点的水平距离是40m,竖直高度是30m.
(1)、若 , 求的半径;(2)、连接 , 求证:四边形是平行四边形.25. 跳台滑雪是冬季奥运会的比赛项目之一,如图,运动员通过助滑道后在点处起跳经空中飞行后落在着陆坡上的点处,他在空中飞行的路线可以看作抛物线的一部分,这里表示起跳点到地面的距离,表示着陆坡的高度,表示着陆坡底端到点的水平距离,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度(单位:m)与水平距离(单位:m)近似满足函数关系: , 已知 , , 落点的水平距离是40m,竖直高度是30m.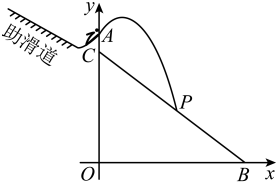 (1)、点的坐标是 , 点的坐标是;(2)、求满足的函数关系;(3)、运动员在空中飞行过程中,当他与着陆坡竖直方向上的距离达到最大时,直接写出此时的水平距离.26. 在平面直角坐标系中,抛物线的对称轴为直线 , 且 .(1)、当时,求的值;(2)、点 , , 在抛物线上,若 , 判断 , 与的大小关系,并说明理由.27. 如图,在中, , , , 连接 , 将线段绕点顺时针旋转90°得到线段 , 连接 .
(1)、点的坐标是 , 点的坐标是;(2)、求满足的函数关系;(3)、运动员在空中飞行过程中,当他与着陆坡竖直方向上的距离达到最大时,直接写出此时的水平距离.26. 在平面直角坐标系中,抛物线的对称轴为直线 , 且 .(1)、当时,求的值;(2)、点 , , 在抛物线上,若 , 判断 , 与的大小关系,并说明理由.27. 如图,在中, , , , 连接 , 将线段绕点顺时针旋转90°得到线段 , 连接 .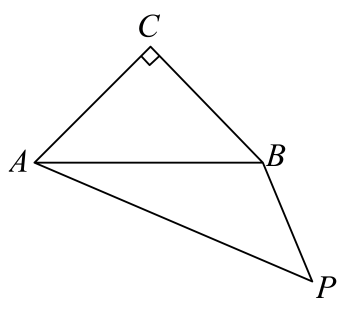 (1)、依题意,补全图形,并证明:;(2)、求的度数;(3)、若为线段的中点,连接 , 请用等式表示线段与之间的数量关系,并证明.28. 给定图形和点 , , 若图形上存在两个不重合的点 , , 使得点关于点的对称点与点关于点的对称点重合,则称点与点关于图形双对合.在平面直角坐标系中,已知点 , , .(1)、在点 , , 中,与点关于线段双对合的点是;(2)、点是轴上一动点,的直径为1.
(1)、依题意,补全图形,并证明:;(2)、求的度数;(3)、若为线段的中点,连接 , 请用等式表示线段与之间的数量关系,并证明.28. 给定图形和点 , , 若图形上存在两个不重合的点 , , 使得点关于点的对称点与点关于点的对称点重合,则称点与点关于图形双对合.在平面直角坐标系中,已知点 , , .(1)、在点 , , 中,与点关于线段双对合的点是;(2)、点是轴上一动点,的直径为1.①若点与点关于双对合,求的取值范围;
②当点运动时,若上存在一点与上任意一点关于双对合,直接写出点的横坐标的取值范围.