山西省吕梁市汾阳市2022-2023学年八年级上学期期末考试数学试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段不能组成三角形的是（）

A、2，3，6 B、5，8，10 C、4，4，7 D、3，4，5

查看试题解析
2. 下列四个图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(- 2 a)}^{2} = 4 a^{2}$ B、 $x^{4} \cdot x^{4} = x^{16}$ C、 ${(- b)}^{7} \div b^{5} = b^{2}$ D、 ${(m^{2})}^{3} \cdot m^{4} = m^{9}$

查看试题解析
4. 如图，A， $B$ 是池塘两侧端点，在池塘的一侧选取一点 $O$ ，测得 $O A$ 的长为6米， $O B$ 的长为6米， $∠ O = 60 °$ ，则A， $B$ 两点之间的距离是（）

A、4米 B、6米 C、8米 D、10米

查看试题解析
5. 如图，衣架框内部可以近似看成一个等腰三角形，记为等腰三角形 $A B C$ ，若 $A B = A C = 26 c m$ ， $D$ 是 $B C$ 的中点， $∠ A B C = 30 °$ ，则 $A D$ 的长为（）

A、 $11 c m$ B、 $12 c m$ C、 $13 c m$ D、 $14 c m$

查看试题解析
6. “春江潮水连海平，海上明月共潮生”，水是诗人钟爱的意象，经测算，一个水分子的直径约为 $0.0000000004 m$ ，数据 $0.0000000004$ 用科学记数法表示为（）

A、 $4 \times 1 0^{- 11}$ B、 $4 \times 1 0^{- 10}$ C、 $4 \times 1 0^{- 9}$ D、 $0.4 \times 1 0^{- 9}$

查看试题解析
7. 如图，这是平面镜成像的示意图，若以蜡烛的底部和平面镜中像的底部连线为 $x$ 轴，平面镜所在点的竖线为 $y$ 轴（镜面厚度忽略不计）建立平面直角坐标系，某时刻火焰顶部 $S$ 的坐标是 $(- 1.5 ， 1)$ ，则此时对应的虚像 $S^{'}$ 的坐标是（）

A、 $(1.5 ， - 1)$ B、 $(1 ， 1.5)$ C、 $(1 ， - 1.5)$ D、 $(1.5 ， 1)$

查看试题解析
8. 下列分式中与 $\frac{- x + y}{- x - y}$ 的值相等的分式是（）

A、 $\frac{x + y}{x - y}$ B、 $\frac{x - y}{x + y}$ C、- $\frac{x + y}{x - y}$ D、- $\frac{x - y}{x + y}$

查看试题解析
9. 如图， $△ A B C ≌ △ A^{^{'}} B C^{^{'}}$ ，过点 $C$ 作 $C D ⊥ B C^{'}$ ，垂足为 $D$ ，若 $∠ A B A^{'} = 55 °$ ，则 $∠ B C D$ 的度数为（）

A、 $25 °$ B、 $35 °$ C、 $45 °$ D、 $55 °$

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ A B C = 60 °$ ， $B D$ 平分 $∠ A B C$ ， $∠ B C D > ∠ C B D$ ， $B C = 24$ ， $P$ ， $Q$ 分别是 $B D$ ， $B C$ 上的动点，当 $C P + P Q$ 取得最小值时， $B Q$ 的长是（）

A、8 B、10 C、12 D、16

查看试题解析

二、填空题

11. 分解因式： $3 a^{2} - 3 =$ .

查看试题解析
12. 如图， $A B$ 与 $O M$ 相交于点 $A$ ，与 $O N$ 相交于点 $B$ ， $O P ⊥ A B$ ，垂足为 $P$ ．现要证明 $△ A O P ≅ △ B O P$ ，若只添加一个条件，这个条件可以是．（不作辅助线，写出一个即可）

查看试题解析
13. 若一个正多边形的外角与其相邻的内角之比为 $1 ： 5$ ，则该正多边形的内角和的度数为．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别是 $(- 3 ， 0)$ ， $(0 ， 2)$ ， $△ O A^{'} B^{'} ≅ △ A O B$ ，若点 $A^{'}$ 在 $x$ 轴的正半轴上，则位于第四象限的点 $B^{'}$ 的坐标是．

查看试题解析
15. 若关于 $x$ 的方程 $\frac{2}{x} = \frac{m}{2 x + 1}$ 无解，则 $m$ 的值为．

查看试题解析

三、解答题

16. 计算：

(1)、 $2^{- 1} + 2^{3} + {(π - 1)}^{0}$ ．

(2)、 $(x + 3 y) (3 x - y) + 3 y^{2}$ ．

查看试题解析
17. 如图，已知 $△ A B C$ ， $D$ 是 $A B$ 延长线上一点， $B D = C B$ ， $D E ∥ B C$ ， $D E = B A$ ，连接 $B E$ ，求证： $B E = C A$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、在 $A C$ 上求作一点 $F$ ，使点 $F$ 到A， $B$ 两点之间的距离相等．（要求：尺规作图，不写作法，保留作图痕迹，标明字母）

(2)、连接 $B F$ ，若 $∠ A = 50 °$ ，求 $∠ F B C$ 的度数．

查看试题解析
19. 在学校开展的“劳动创造美好生活”主题活动中，八（1）班负责校园某绿化角的设计、种植与养护，同学们计划购买绿萝和吊兰两种绿植，已知吊兰的单价比绿萝的单价多5元，且用200元购买绿萝的盆数与用300元购买吊兰的盆数相同．

(1)、求购买绿萝和吊兰的单价各是多少元？

(2)、若购买绿萝的数量是吊兰数量的两倍，且资金不超过600元，则购买吊兰的数量最多是多少盆？

查看试题解析
20. 如图

(1)、证明角平分线具有的性质：角平分线上的点到角的两边的距离相等．为了更直观、清楚地表达题意，我们通常在证明之前画出图形，并用符号表示已知和求证．如图1，已知： $O C$ 平分 $∠ A O B$ ，点 $P$ 在 $O C$ 上， $P D ⊥ O A$ ， $P E ⊥ O B$ ，垂足分别为 $D$ ， $E$ ．求证： $P D = P E$ ．

(2)、如图2，在 $△ O A B$ 中， $O P$ 平分 $∠ A O B$ ，交 $A B$ 于点 $P$ ， $P D ⊥ O A$ 于点 $D$ ， $P E ⊥ O B$ 于点 $E$ ， $O A = O B = 6$ ，若 $S_{△ O A B} = 15$ ，求 $P D$ 的长．

查看试题解析
21. 动点问题是数学学习中常见的问题，解决此类问题的关键是动中求静，运用分类讨论及数形结合的思想灵活解决问题．如图，在等边三角形 $A B C$ 中， $B C = 6 c m$ ，点 $P$ 在线段 $B A$ 上从点B出发向点A运动（点 $P$ 不与点 $A$ 重合），点 $P$ 运动的速度为 $2 c m / s$ ；点 $Q$ 在线段 $C B$ 上从点 $C$ 出发向点B运动（点 $Q$ 不与点B重合），点 $Q$ 运动的速度为 $3 c m / s$ ，设点 $P$ ， $Q$ 同时运动，运动时间为 $t s$ ．

(1)、在点 $P$ ， $Q$ 运动过程中，经过几秒时 $△ P B Q$ 为等边三角形？

(2)、在点 $P$ ， $Q$ 运动过程中，若某时刻 $△ P B Q$ 为直角三角形，请计算运动时间 $t$ ．

查看试题解析
22. 有足够多的长方形和正方形卡片（如图1），分别记为1号，2号，3号卡片．

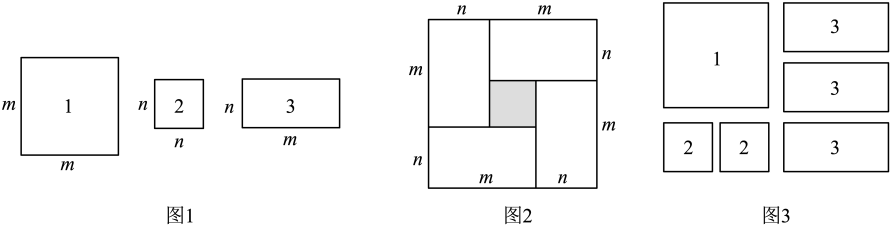(1)、如果选取4张3号卡片，拼成如图2所示的一个正方形，请用2种不同的方法表示阴影部分的面积（用含 $m$ ， $n$ 的式子表示）．
①方法1：；方法2：；
②请写出 ${(m + n)}^{2}$ ， ${(m - n)}^{2}$ ， $4 m n$ 三个代数式之间的等量关系：．

(2)、若 $| a + b - 6 | + | a b - 4 | = 0$ ，求 ${(a - b)}^{2}$ 的值．

(3)、如图3，选取1张1号卡片，2张2号卡片，3张3号卡片，可拼成一个长方形（无缝隙不重叠），请画出该长方形，根据图形的面积关系，分解因式： $m^{2} + 3 m n + 2 n^{2} =$ ．

查看试题解析
23. 综合与探究
问题提出：某兴趣小组在综合与实践活动中提出这样一个问题：在等腰直角三角板 $A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $D$ 为 $B C$ 的中点，用两根小木棒构建角，将顶点放置于点 $D$ 上，得到 $∠ M D N$ ，将 $∠ M D N$ 绕点 $D$ 旋转，射线 $D M$ ， $D N$ 分别与边 $A B$ ， $A C$ 交于 $E$ ， $F$ 两点，如图1所示．

(1)、操作发现：如图2，当 $E$ ， $F$ 分别是 $A B$ ， $A C$ 的中点时，试猜想线段 $D E$ 与 $D F$ 的数量关系是，位置关系是．

(2)、类比探究：如图3，当 $E$ ， $F$ 不是 $A B$ ， $A C$ 的中点，但满足 $B E = A F$ 时，判断 $△ D E F$ 的形状，并说明理由．

(3)、拓展应用：①如图4，将 $∠ M D N$ 绕点 $D$ 继续旋转，射线 $D M$ ， $D N$ 分别与 $A B$ ， $C A$ 的延长线交于 $E$ ， $F$ 两点，满足 $B E = A F$ ， $△ D E F$ 是否仍然具有（2）中的情况？请说明理由；
②若在 $∠ M D N$ 绕点 $D$ 旋转的过程中，射线 $D M$ ， $D N$ 分别与直线 $A B$ ， $C A$ 交于 $E$ ， $F$ 两点，满足 $B E = A F$ ，若 $A B = a$ ， $B E = b$ ，则 $A E =$ ▲ （用含 $a$ ， $b$ 的式子表示）．

查看试题解析