辽宁省沈阳市铁西区2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，属于无理数的是（）

A、 $\sqrt{2}$ B、0.5 C、 $\frac{1}{3}$ D、 $\sqrt{4}$

查看试题解析
2. 如图，直线l₁、l₂分别与△ABC的两边AB、BC相交，且l₁∥l₂ ，若∠B＝35°，∠1＝105°，则∠2的度数为（）

A、45° B、50° C、40° D、60°

查看试题解析
3. 若二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、 $x > 1$ B、 $x ≥ 1$ C、 $x < 1$ D、 $x \leq 1$

查看试题解析
4. 下列各组数据中的三个数，可作为三边长构成直角三角形的是（）

A、1、2、3 B、7、8、9 C、6、8、10 D、5、12、20

查看试题解析
5. 估计 $\sqrt{10}$ +1的值应在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
6. 下列计算正确的是（　　）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$

查看试题解析
7. 如图，在△ABC中，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，∠D＝15°，则∠A的度数为（）

A、30° B、45° C、20° D、22.5°

查看试题解析
8. 如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则关于x，y的方程组 ${\begin{matrix} y = 2 x \\ y = a x + 4 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = \frac{3}{2} \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 3 \\ y = \frac{3}{2} \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
9. 随着冬季的来临，流感进入高发期.某校为有效预防流感，购买了A，B，C，D四种艾条进行消毒，它们的单价分别是30元，25元，20元，18元.四种艾条的购买比例如图所示，那么所购买艾条的平均单价是（　　）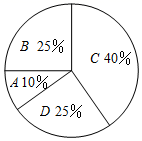

A、22.5元 B、23.25元 C、21.75元 D、24元

查看试题解析
10. 已知点（﹣2，y₁），（3，y₂）都在直线y＝﹣x﹣5上，则y₁ ， y₂的值的大小关系是（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、不能确定

查看试题解析

二、填空题

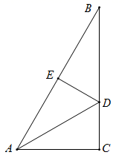
11. 在平面直角坐标系中，点 $A (- 2 ， 3)$ 关于y轴对称后的点的坐标为．

查看试题解析
12. 计算 $\sqrt{4^{2}}$ 的结果是．

查看试题解析
13. 甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是1.28m，方差分别是S_甲²＝0.60，S_乙²＝0.62，S_丙²＝0.58，S_丁²＝0.45，则这四名同学跳高成绩最稳定的是．

查看试题解析
14. 比较两数的大小：2 $\sqrt{3}$ 3．（填“＜”或“＞”）

查看试题解析
15. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $D E ⊥ A B$ 于E， $∠ B = 30 °$ ，若 $D E$ =2，则 $C B$ 的长等于．

查看试题解析
16. 如图，直线 $y = \frac{4}{3} x + 8$ 与x轴、y轴分别交于点B和点A，点C是线段 $O A$ 上的一点，若将 $△ A B C$ 沿 $B C$ 折叠，点A恰好落在x轴上的 $A ′$ 处，若P是y轴负半轴上一动点，且 $△ B C P$ 是等腰三角形，则P的坐标为．

查看试题解析

三、解答题

17. $\sqrt{32} - 4 \sqrt{\frac{1}{2}} + \sqrt{2}$ ．

查看试题解析
18. 解方程组： ${\begin{matrix} 2 x - y = 3 \\ 3 x + 2 y = 8 \end{matrix}$ ．

查看试题解析
19. 如图所示，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别是 $A (a ， - 4)$ ， $B (- 1 ， 2)$ 和 $C (- 4 ， 4)$ ．

(1)、已知点 $A (a ， - 4)$ 关于x轴的对称点P的坐标为 $(- 5 ， b)$ ，则 $a =$ ， $b =$ ；

(2)、画出 $△ A B C$ ，则 $△ A B C$ 的面积为 ▲ ；点C到AB的距离为 ▲ ；

查看试题解析
20. 2021年6月26日是第34个国际禁毒日，为了解同学们对禁毒知识的掌握情况，学校开展了禁毒知识讲座和知识竞赛，从全校1800名学生中随机抽取部分学生的竞赛试卷进行调查分析，并将成绩（满分：100分）制成如图所示的扇形统计图和条形统计图．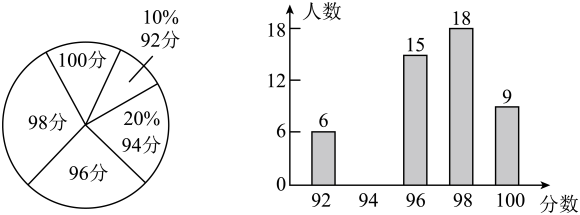
请根据统计图回答下列问题：

(1)、求出随机被抽查的学生总数，并补全上面不完整的条形统计图；

(2)、这些学生成绩的中位数是分；众数是分；

(3)、根据比赛规则，96分以上的学生有资格进入第二轮知识竞赛环节，请你估计全校1800名学生进入第二轮环节的人数是多少？

查看试题解析
21. 某超市计划购进一批玩具，有甲、乙两种玩具可供选择，已知1件甲种玩具与1件乙种玩具的进价之和为57元，2件甲种玩具与3件乙种玩具的进价之和为141元．

(1)、甲、乙两种玩具每件的进价分别是多少元？

(2)、现在购进甲种玩具有优惠，优惠方案是：若购进甲种玩具超过20件，则超出部分可以享受7折优惠．设购进a（a＞20）件甲种玩具需要花费w元，请求出w与a的函数关系式．

查看试题解析
22. 如图1，在等腰 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点P在边 $A B$ 上，将射线 $C P$ 绕点C逆时针旋转 $45 °$ ，交 $A B$ 于点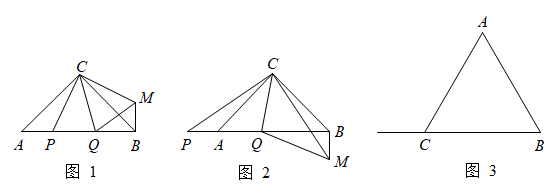Q，再将 $△ C A P$ 绕点C逆时针旋转 $90 °$ 得 $△ C B M$ ，连接 $Q M$ ．根据以上操作可知： $∠ Q C M = 45 °$ ， $△ C P Q ≌ △ C M Q$ ．

(1)、将点P移动到边 $B A$ 的延长线上，重复上述操作得到图2，根据操作，判断 $A P$ 、 $P Q$ 、 $B Q$ 之间的数量关系，并说明理由．

(2)、如图3，等腰 $R t △ A B C$ 改为等边 $△ A B C$ 且 $A B = 2$ ，点P为射线BC上一动点，将射线AP绕点A逆时针旋转 $30 °$ ，交射线BC于点Q，再将 $△ A P C$ 绕点A逆时针旋转60°得 $△ A M B$ ，当 $△ B M Q$ 为直角三角形时，请直接写出 $C P$ 的长．

查看试题解析
23. 如图1，直线 $y = \frac{1}{3} x + 2$ 与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．

(1)、求直线 $B C$ 的函数表达式；

(2)、设点M是x轴上的一个动点，过点M作y轴的平行线，交直线 $A B$ 于点P，交直线 $B C$ 于点Q，连接 $B M$ ．
①若 $∠ M B C = 90 °$ ，请直接写出点P的坐标；
②若 $△ P Q B$ 的面积为 $\frac{9}{8}$ ，请直接写出点M的坐标；
③若点K为线段 $O B$ 的中点，连接 $C K$ ，如图2，若在线段 $O C$ 上有一点F，满足 $∠ C K F = 45 °$ ，请直接写出点F的坐标．

查看试题解析