辽宁省大连市沙河口区2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 若代数式 $\frac{1}{x - 2}$ 有意义，则实数x的取值范围是（）

A、 $x = 0$ B、 $x = 2$ C、 $x \neq 0$ D、 $x \neq 2$

查看试题解析
2. 三角形的三边长可以是（）

A、2，11，13 B、5，12，7 C、5，5，11 D、5，12，13

查看试题解析
3. 下列运算错误的是（）

A、 $x^{2} \cdot x^{3} = x^{5}$ B、 ${(x^{2})}^{3} = x^{6}$ C、 $x^{3} + x^{2} = 2 x^{6}$ D、 ${(- 2 x)}^{3} = - 8 x^{3}$

查看试题解析
4. 若等腰三角形的周长为30cm，一边为14cm，则腰长为（）

A、2cm B、8cm C、8cm或2cm D、14cm或8cm

查看试题解析
5. 下列从左到右的变形是因式分解的是（）

A、 $(y - 1) (y - 2) = y^{2} - 3 y + 2$ B、 $a^{2} + 2 a x + x^{2} = a (a - 2 x) + x^{2}$ C、 $x^{2} + 2 x + 1 = {(x + 1)}^{2}$ D、 $(x + 3) (x - 3) = x^{2} - 9$

查看试题解析
6. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

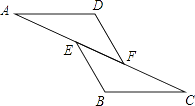A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC

查看试题解析
7. 已知一个多边形的内角和为1080°，则这个多边形是（）

A、九边形 B、八边形 C、七边形 D、六边形

查看试题解析
8. 已知 $x^{2} + m x + 9$ 是完全平方式，则 $m$ 的值是（）

A、6 B、-6 C、±3 D、±6

查看试题解析
9. 货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x千米/小时，依题意列方程正确的是（）

A、 $\frac{25}{x} = \frac{35}{x - 20}$ B、 $\frac{25}{x - 20} = \frac{35}{x}$ C、 $\frac{25}{x} = \frac{35}{x + 20}$ D、 $\frac{25}{x + 20} = \frac{35}{x}$

查看试题解析
10. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法中正确的个数是
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S_△DAC：S_△ABC=1：3．

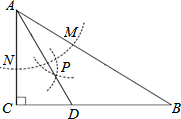A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算： $3^{- 2}$ =.

查看试题解析
12. 一个长方形的面积为 $a^{2} + a$ ，宽为a，则长方形的长为．

查看试题解析
13. 因式分解： $x y^{2} - 4 x$ = ．

查看试题解析
14. 若x+y＝6，xy＝7，则x²+y²的值等于．

查看试题解析
15. 已知点 $P (a ， 2 a - 3)$ 关于 $x$ 轴对称的点在第一象限，则 $a$ 的取值范围是．

查看试题解析
16. 如图， $B D$ 是 $△ A B C$ 的角平分线， $A E ⊥ B D$ ，垂足为 $F$ ，连结 $D E$ ．若 $∠ A B C = 36 °$ ， $∠ C = 44 °$ ，则 $∠ E A D$ 的度数为．

查看试题解析

三、解答题

17. 计算题：

(1)、 $\frac{1}{2} a b^{2} \cdot (- 6 a b c)$ ；

(2)、 ${(x - 2 y)}^{2} - (x - y) (x + y)$ ．

查看试题解析
18. 先化简再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} + 2 x + 1}{x^{2} - 4}$ ，其中 $x = 1$ ．

查看试题解析
19. 如图，C是路段AB的中点，两人从C同时出发，以相同的速度分别沿两条直线行走，并同时到达D，E两地，DA⊥AB，EB⊥AB，D，E与路段AB的距离相等吗？为什么？

查看试题解析
20. 如图，在△ABC中， $A B = A C$ ，点D在 $A B$ 上，且点D到点A的距离与点D到点C的距离相等．

(1)、利用尺规作图作出点D，不写作法但保留作图痕迹；

(2)、连接 $C D$ ，若 $△ A B C$ 的底边长为2，周长为 $9.4$ ，求 $△ B C D$ 的周长．

查看试题解析
21. 某工程队准备为公园修建一条长 $1200 m$ 的跑道，由于采用新的施工方式，实际每天修建跑道的长度比原计划增加 $25 %$ ，结果提前2天完成这一任务，求原计划每天修建跑道多少米？

查看试题解析
22. 如图，在五边形 $A B C D E$ 中， $A B = D E$ ， $A C = A D$ ．

(1)、请你添加一个条件，使得 $△ A B C ≌ △ D E A$ ，并说明理由；

(2)、在(1)的条件下，若 $∠ C A D = 66 °$ ， $∠ B = 110 °$ ，求 $∠ B A E$ 的度数．

查看试题解析
23. 如图，某市有一块长 $(3 a + b) m$ ，宽 $(2 a + b) m$ 的长方形地块，规划部门计划将阴影部分进行绿化，在中间正方形空白处修建一个喷水池．

(1)、求绿化的面积；

(2)、当 $a = 2$ ， $b = 1$ 时，绿化的面积是多少 $m^{2}$ ？

查看试题解析
24. 如图1，平面直角坐标系中， $A B ∥ x$ 轴， $O A = A B$ ， C是点A关于x轴的对称点， $B C ∥ O A$ ，交x轴于点E，连接 $O B$ ．

(1)、求证：
① $O B$ 平分 $∠ A O E$ ；
② $△ O C E$ 是等边三角形；

(2)、如图2，若F在 $O B$ 上， $∠ B A F = 45 °$ ，连接 $C F$ ，点B的坐标为 $(a ， b)$ ，直接写出点F的坐标（用a、b表示）．

查看试题解析
25. 数学活动课上，老师出示了一个问题：如图1，等腰 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = A C$ ，点D为 $A C$ 上一点，过点A作 $A E ∥ B D$ ， $A E = B F$ ， $A E ⊥ E F$ ， $E F$ 交 $A B$ 于点P，大家通过思考与实践，纷纷提出不同的问题．

(1)、小明说： $P E$ 与 $P F$ 有一定数量关系，试说出小明的猜想，并加以证明；

(2)、小伟说：如图2，连接 $C E$ ，如果 $C E = A C$ ，则 $A E = E F$ ，请帮助小伟加以证明；

(3)、小超受小伟的启发，在小伟添加的条件下，也提出一个问题：如图3，在 $B D$ 上取点Q，使 $∠ E C Q = 45 °$ ，若 $A E = 6$ ，求 $Δ B C Q$ 的面积，请你思考此问题，并解决此问题．

查看试题解析