湖北省孝感市孝昌县2022-2023学年八年级上学期期末质量检测数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、4. 下列等式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 若分式 的值为0,则x的值为( )A、-1 B、0 C、1 D、±16. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递40件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )A、= B、 C、=﹣40 D、=7.
2. 下列计算正确的是( )A、 B、 C、 D、3. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、4. 下列等式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 若分式 的值为0,则x的值为( )A、-1 B、0 C、1 D、±16. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递40件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )A、= B、 C、=﹣40 D、=7.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
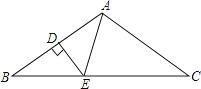 A、80° B、60° C、50° D、40°8. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )
A、80° B、60° C、50° D、40°8. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )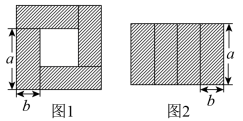 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
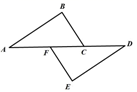
9. 已知点 , 是关于x轴对称的点,a-b= .10. 如图,在△ABC和△FED,A、F、C、D在同一直线上,AC=FD,AB=DE,当添加条件时,就可得到△ABC≌△DEF;(只需填写一个你认为正确的条件即可)
 11. 20200= .12. 已知a+b=5,ab=3, = .13. 计算:= .14. 如图,在中,点在边上, . 若 , 则的大小为度.
11. 20200= .12. 已知a+b=5,ab=3, = .13. 计算:= .14. 如图,在中,点在边上, . 若 , 则的大小为度.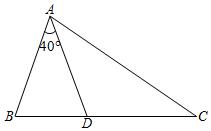 15. 若 , , 则ab= .16. 若分式 有意义,则x的取值范围是 .
15. 若 , , 则ab= .16. 若分式 有意义,则x的取值范围是 .
三、解答题
-
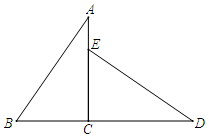
17. 分解因式:(1)、 .(2)、 .18. 解下列分式方程:(1)、(2)、19. 先化简,再求值: ,其中 .20. 如图,AC⊥BD,DE交AC于E,AB=DE,∠A=∠D.求证:AC=AE+BC.
 21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),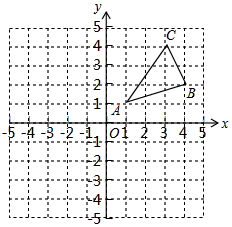
⑴画出△ABC关于y轴的对称图形△A1B1C1 , 并写出点B1的坐标;
⑵在x轴上求作一点P , 使△PAB的周长最小,并直接写出点P的坐标.
22.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
 (1)、求证:△ABC≌△AED;(2)、当∠B=140°时,求∠BAE的度数.23. 某校为了创建书香校远,计划进一批图书,经了解.文学书的单价比科普书的单价少20元,用800元购进的文学书本数与用1200元购进的科普书本数相等.(1)、文学书和科普书的单价分别是多少元?(2)、该校计划用不超过5000元的费用购进一批文学书和科普书,问购进60本文学书后最多还能购进多少本科普书?24. 如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接MC.
(1)、求证:△ABC≌△AED;(2)、当∠B=140°时,求∠BAE的度数.23. 某校为了创建书香校远,计划进一批图书,经了解.文学书的单价比科普书的单价少20元,用800元购进的文学书本数与用1200元购进的科普书本数相等.(1)、文学书和科普书的单价分别是多少元?(2)、该校计划用不超过5000元的费用购进一批文学书和科普书,问购进60本文学书后最多还能购进多少本科普书?24. 如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接MC.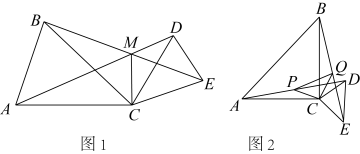 (1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数(直接写出结果);(3)、当时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.
(1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数(直接写出结果);(3)、当时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.