河北省廊坊市安次区2022-2023学年八年级上学期期末数学测试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 钢架雪车是年北京冬奥会的比赛项目之一.下面这些钢架雪车运动标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 关于全等图形的描述,下列说法正确的是( )A、形状相同的图形 B、面积相等的图形 C、能够完全重合的图形 D、周长相等的图形3. 若分式有意义,则a的取值范围是( )A、 B、 C、 D、4. 在平面直角坐标系中,点关于y轴对称的点的坐标为( )A、 B、 C、 D、5. 如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )
2. 关于全等图形的描述,下列说法正确的是( )A、形状相同的图形 B、面积相等的图形 C、能够完全重合的图形 D、周长相等的图形3. 若分式有意义,则a的取值范围是( )A、 B、 C、 D、4. 在平面直角坐标系中,点关于y轴对称的点的坐标为( )A、 B、 C、 D、5. 如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )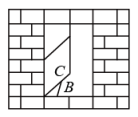 A、三角形具有稳定性 B、两点确定一条直线 C、两点之间线段最短 D、三角形的两边之和大于第三边6. 下列各式变形正确的是( )A、 B、 C、 D、7. 下列多边形中,内角和为540°的是( )A、
A、三角形具有稳定性 B、两点确定一条直线 C、两点之间线段最短 D、三角形的两边之和大于第三边6. 下列各式变形正确的是( )A、 B、 C、 D、7. 下列多边形中,内角和为540°的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( )
8. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( ) A、18 B、12 C、6 D、99. 如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )
A、18 B、12 C、6 D、99. 如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )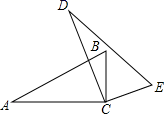 A、20° B、40° C、70° D、90°10. 如图, , 的周长为9,的垂直平分线交于点E,垂足为D,则( )
A、20° B、40° C、70° D、90°10. 如图, , 的周长为9,的垂直平分线交于点E,垂足为D,则( ) A、6 B、5 C、4 D、911. 分式与的最简公分母是( )A、 B、 C、 D、12. 若能用完全平方公式进行因式分解,则常数m的值为 ( )A、1或5 B、7或-1 C、5 D、713. 如图,已知是等边三角形,点在同一直线上,且 , , 则的度数为( )
A、6 B、5 C、4 D、911. 分式与的最简公分母是( )A、 B、 C、 D、12. 若能用完全平方公式进行因式分解,则常数m的值为 ( )A、1或5 B、7或-1 C、5 D、713. 如图,已知是等边三角形,点在同一直线上,且 , , 则的度数为( ) A、 B、 C、 D、14. 下列计算正确的是( )A、 B、 C、 D、15. 嘉淇在解决问题时,给出的推理过程如下:
A、 B、 C、 D、14. 下列计算正确的是( )A、 B、 C、 D、15. 嘉淇在解决问题时,给出的推理过程如下:如图,点D在上,点E在上, , ,
求证:.
证明:在和中, ,
∴ , ∴.

小明为保证嘉淇的推理更严谨,想在方框中“∴”和“∴”之间作补充,下列说法正确的是 ( )
A、嘉淇的推理严谨,不需要补充 B、应补充“∴” C、应补充“∴” D、应补充“∴”16. 某工程需要在规定时间内完成,如果甲工程队单独做,恰好如期完成; 如果乙工程队单独做,则多用天,现在甲、乙两队合做天,剩下的由乙队单独做,恰好如期完成,求规定时间.如果设规定日期为天,下面所列方程中错误的是( )A、 B、 C、 D、二、填空题
-
17. 在△ABC中,若∠A=30°,∠B=50°,则∠C= .18. 在如图所示的方格中,以为边,第三个顶点也在格点上的等腰三角形有个.

三、解答题
-
19. 如图,学校劳动实践基地有两块边长分别为 , 的正方形秧田 , , 其中不能使用的面积为 .
 (1)、用含 , 的代数式表示中能使用的面积;(2)、若 , , 求比多出的使用面积.20.(1)、解方程:(2)、先化简,再求值: , 其中 .21. 在中, , .(1)、若是整数,求的长.(2)、已知是的中线,若的周长为10,求三角形的周长.22. 如图,在平面直角坐标系中,的顶点坐标分别为 .
(1)、用含 , 的代数式表示中能使用的面积;(2)、若 , , 求比多出的使用面积.20.(1)、解方程:(2)、先化简,再求值: , 其中 .21. 在中, , .(1)、若是整数,求的长.(2)、已知是的中线,若的周长为10,求三角形的周长.22. 如图,在平面直角坐标系中,的顶点坐标分别为 . (1)、画出关于y轴对称的;(2)、写出(1)中所画的的各顶点坐标;(3)、连接 , 则四边形的面积为 .23. 如图,已知点B,E,C,F在一条直线上, , , .
(1)、画出关于y轴对称的;(2)、写出(1)中所画的的各顶点坐标;(3)、连接 , 则四边形的面积为 .23. 如图,已知点B,E,C,F在一条直线上, , , . (1)、求证:;(2)、若 , , 求的长.24. 刘芳和李婷进行跳绳比赛.已知刘芳每分钟比李婷多跳20个,刘芳跳135个所用的时间与李婷跳120个所用的时间相等.求李婷每分钟跳绳的个数.25. 如图(1),大正方形的面积可以表示为 , 同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即 . 同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式: . 把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)、求证:;(2)、若 , , 求的长.24. 刘芳和李婷进行跳绳比赛.已知刘芳每分钟比李婷多跳20个,刘芳跳135个所用的时间与李婷跳120个所用的时间相等.求李婷每分钟跳绳的个数.25. 如图(1),大正方形的面积可以表示为 , 同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即 . 同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式: . 把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”. (1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个等式:;(2)、如图(3),中, , , , , 是斜边边上的高.用上述“面积法”求的长;(3)、如图(4),等腰中, , 点为底边上任意一点, , , , 垂足分别为点 , , , 连接 , 用上述“面积法”求证: .26. 已知△ABC是边长为4的等边三角形,点D是射线BC上的动点,将AD绕点A逆时针方向旋转60°得到AE,连接DE.
(1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个等式:;(2)、如图(3),中, , , , , 是斜边边上的高.用上述“面积法”求的长;(3)、如图(4),等腰中, , 点为底边上任意一点, , , , 垂足分别为点 , , , 连接 , 用上述“面积法”求证: .26. 已知△ABC是边长为4的等边三角形,点D是射线BC上的动点,将AD绕点A逆时针方向旋转60°得到AE,连接DE. (1)、如图1,猜想△ADE是什么三角形?;(直接写出结果)(2)、如图2,猜想线段CA、CE、CD之间的数量关系,并证明你的结论;(3)、在点D运动过程中,△DEC的周长是否存在最小值?若存在,请求出△DEC周长的最小值;若不存在,请说明理由.
(1)、如图1,猜想△ADE是什么三角形?;(直接写出结果)(2)、如图2,猜想线段CA、CE、CD之间的数量关系,并证明你的结论;(3)、在点D运动过程中,△DEC的周长是否存在最小值?若存在,请求出△DEC周长的最小值;若不存在,请说明理由.