北京市平谷区2022-2023学年八年级上学期数学期末试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 以下四个标志中，是轴对称图形的是（）

A、绿色食品 B、循环回收 C、节能 D、节水

查看试题解析
2. 4的算术平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
3. 下列分式中是最简分式的是（）

A、 $\frac{2 x}{4 x^{2}}$ B、 $\frac{x^{2} + y^{2}}{x + y}$ C、 $\frac{x^{2} + 2 x + 1}{x + 1}$ D、 $\frac{x^{2} - 4}{x + 2}$

查看试题解析
4. 为估计池塘两岸A、B间的距离，如图，小明在池塘一侧选取了点O，测得 $O A = 8 m ， O B = 15 m$ ，那么A、B间的距离不可能是（）

A、 $7 m$ B、 $13 m$ C、 $14 m$ D、 $15 m$

查看试题解析
5. 下列说法正确的是（）

A、在10万次试验中，每次都发生了的事件是必然事件 B、必然事件是在10万次试验中，每次都发生 C、在10万次试验中，每次都没有发生的事件是不可能事件 D、任意掷一枚骰子，面朝上的点数大于6，是随机事件

查看试题解析
6. 若 $m = \sqrt{7}$ ，估计m的值所在的范围是（）

A、 $0 < m < 1$ B、 $1 < m < 2$ C、 $2 < m < 3$ D、 $3 < m < 4$

查看试题解析
7. 如图， $R t △ A B C$ 中， $∠ A = 90 °$ ， $B P$ 平分 $∠ A B C$ 交 $A C$ 于点P，若 $P A = 4 c m$ ， $B C = 13 c m$ ，则 $△ B C P$ 的面积是（）

A、 $52 c m^{2}$ B、 $13 c m^{2}$ C、 $45 c m^{2}$ D、 $26 c m^{2}$

查看试题解析
8. 如图，等边 $△ A B D$ 和等边 $△ B C E$ 中，A、B、C三点共线， $A E$ 和 $C D$ 相交于点F，下列结论中正确的个数是（）
① $△ A B E ≅ △ D B C$ ；② $B F$ 平分 $∠ A F C$ ；③ $A F = D F + B F$ ；④ $∠ A F D = 60 °$

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则实数 $x$ 的取值范围是.

查看试题解析
10. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为零，则x的值为．

查看试题解析
11. 命题“等边对等角”的逆命题是，是（填“真命题”或 “假命题”）．

查看试题解析
12. 如图， $△ A B C$ 中， $A B = A C$ ， D是BA延长线上一点，且 $∠ D A C = 100 °$ ，则 $∠ C =$ ．

查看试题解析
13. 在一个不透明的口袋中装有除颜色外其它都相同的3个红球和2个黄球，任意从口袋中摸出一个球，摸到黄球的概率为．

查看试题解析
14. 等腰三角形的一个角为80°，则这个等腰三角形的顶角的度数为．

查看试题解析
15. 已知实数 $a$ 在数轴上的位置如图所示，则化简 $| a - 1 | + \sqrt{a^{2}}$ 的结果是．

查看试题解析
16. 如图，在 $△ A B C$ 中，根据尺规作图痕迹，下列四个结论中：① $A F = B F$ ；② $∠ A F D + ∠ F B C = 90 °$ ；③ $D F ⊥ A B$ ；④ $∠ B A F = ∠ C A F$ ．所有正确结论的序号是：．

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{2}{\sqrt{2}} + \sqrt{\frac{4}{3}} \div \sqrt{\frac{1}{3}}$ ；

(2)、 $(\sqrt{2} + 1)^{2} - \sqrt{8}$ ．

查看试题解析
18. 计算： $\sqrt[3]{8} - {(π - \sqrt{3})}^{0} + {(\sqrt{2})}^{2} + | - 2 |$ ．

查看试题解析
19. 计算： $\frac{x^{2} - x}{x^{2} - 2 x + 1} \div (1 + \frac{1}{x - 1})$ ．

查看试题解析
20. 解分式方程： $\frac{x}{x^{2} - 1} + 1 = \frac{x}{x + 1}$ ．

查看试题解析
21. 如图，点P在 $∠ A O B$ 的平分线上， $O A = O B$ ，求证： $A P = B P$ ．

查看试题解析
22. 先化简，再求值： $(\frac{a^{2} + b^{2}}{2 a} - b) \cdot \frac{a}{a - b}$ ，其中 $a - b = 2 \sqrt{3}$ ．

查看试题解析
23. 用直尺和圆规作一个 $45 °$ 的角．
作法：①作直线 $l$ ，在直线 $l$ 上任取一点 $O$ ；
②以 $O$ 为圆心，任意长为半径作弧，交直线 $l$ 于 $M N$ 两点；
③分别以 $M ， N$ 为圆心，大于 $\frac{1}{2} M N$ 的同样长为半径作弧，两弧在直线 $l$ 的上方交于点 $P$ ，作直线 $O P$ ；
④作 $∠ P O N$ 的角平分线 $O A$ ；
所以 $∠ A O N$ 即为所求作的 $45 °$ 角．

(1)、利用直尺和圆规依作法补全图形(保留作图痕迹)；

(2)、完成下面的证明．
证明：连接 $P M$ ， $P N$
$∵$ $P M = P N$ ，
$∴$ 点 $P$ 在线段 $M N$ 的垂直平分线上（）(填推理的依据)．
$∵$ $O M = O N$ ，
$∴$ 点 $O$ 在线段 $M N$ 的垂直平分线上．
$∴$ 直线 $O P$ 是线段 $M N$ 的垂直平分线．
$∴$ $O P ⊥ M N$ ．
∴ $a = \frac{E q}{m}$
∵ $O A$ 平分 $∠ P O N$ ，
∴ $∠ A O N = \frac{1}{2} ∠ P O N = 45 °$ ．

查看试题解析
24. 阅读下面材料：小明遇到这样一个问题：如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线， $E$ 是 $A D$ 上一点，延长 $B E$ 交 $A C$ 于点 $F$ ， $A F = E F$ ，求证： $A C = B E$ ．
小明发现，延长AD到点H，使DH=AD，连结BH，构造 $△ B D H$ ，通过证明 $△ B D H$ 与 $△ A C D$ 全等， $△ B E H$ 为等腰三角形，使问题得以解决（如图2）．请写出推导过程．

查看试题解析
25. 已知： $M = \frac{y}{x}$ ， $N = \frac{y + 1}{x + 1}$ （ $x ， y$ 是正整数）．

(1)、若 $(y - 1)^{2} + \sqrt{x - 2} = 0$ ，求 $M - N$ 的值；

(2)、试比较 $M$ 与 $N$ 的大小．

查看试题解析
26. 如图，在 $Δ A B C$ 中， $A B = 5$ ， $A C = 4$ ， $B C = 3$ ， $D E$ 是 $A B$ 的垂直平分线， $D E$ 分别交 $A C$ ， $A B$ 于点 $E$ ， $D$ ．

(1)、求证： $Δ A B C$ 是直角三角形；

(2)、求 $A E$ 的长．

查看试题解析
27. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = α$ （ $0 ° < α < 90 °$ ）， $A D$ 为 $B C$ 边上的中线，过点 $B$ 作 $B E ⊥ A C$ 于 $E$ ，交 $A D$ 于点 $F$ ，作 $∠ A B E$ 的角平分线 $A D$ 于 $M$ ，交 $A C$ 于 $N$ ．

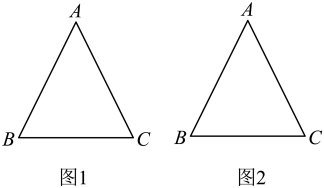(1)、①补全图形1；
②求 $∠ C B E$ 的度数（用含 $α$ 的式子表示）．

(2)、如图2，若 $∠ α = 45 °$ ，猜想 $A F$ 与 $B M$ 的数量关系，并证明你的结论．

查看试题解析
28. 阅读理解：
材料1：为了研究分式 $\frac{1}{x}$ 与其分母x的数量变化关系，小力制作了表格，并得到如下数据：
$x$
…
-4
-3
-2
-1
0
1
2
3
4
…
$\frac{1}{x}$
…
-0.25
$- 0 . \overset{\cdot}{3}$
-0.5
-1
无意义
1
$0.5$
$0 . \overset{\cdot}{3}$
$0.25$
…
从表格数据观察，当 $x > 0$ 时，随着 $x$ 的增大， $\frac{1}{x}$ 的值随之减小，若 $x$ 无限增大，则 $\frac{1}{x}$ 无限接近于0；当 $x < 0$ 时，随着 $x$ 的增大， $\frac{1}{x}$ 的值也随之减小．
材料2：在分子、分母都是整式的情况下，如果分子的次数小于分母的次数，称这样的分式为真分式．如果分子的次数大于或等于分母的次数，称这样的分式为假分式．任何一个假分式都可以化为一个整式与一个真分式的和．例如： $\frac{2 x + 1}{x - 2} = \frac{2 x - 4 + 4 + 1}{x - 2} = \frac{2 (x - 2) + 5}{x - 2} = \frac{2 (x - 2)}{x - 2} + \frac{5}{x - 2} = 2 + \frac{5}{x - 2} ；$
根据上述材料完成下列问题：

(1)、当 $x > 0$ 时，随着 $x$ 的增大， $2 + \frac{1}{x}$ 的值(增大或减小)；当 $x < 0$ 时，随着 $x$ 的增大， $\frac{3 x + 1}{x}$ 的值（增大或减小）；

(2)、当 $x > - 3$ 时，随着 $x$ 的增大， $\frac{2 x + 8}{x + 3}$ 的值无限接近一个数，请求出这个数；

(3)、当 $0 < x < 1$ 时，直接写出代数式 $\frac{3 x - 4}{x - 2}$ 值的取值范围是．

查看试题解析

$x$	…	-4	-3	-2	-1	0	1	2	3	4	…
$\frac{1}{x}$	…	-0.25	$- 0 . \overset{\cdot}{3}$	-0.5	-1	无意义	1	$0.5$	$0 . \overset{\cdot}{3}$	$0.25$	…