安徽省淮南市西部地区2022-2023学年八年级上学期数学期末测试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（　　）

A、 B、 C、 D、

查看试题解析
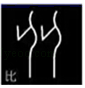2. 一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（　　）

A、13cm B、14cm C、13cm或14cm D、以上都不对

查看试题解析
3. 若分式 $\frac{x - 1}{x + 1}$ 的值为 $0$ ，则 $x =$ （）

A、-1 B、1 C、±1 D、0

查看试题解析
4. 地球的体积约为10¹²立方千米，太阳的体积约为1.4×10¹⁸立方千米，地球的体积是太阳体积的倍数约是（）

A、7.1×10^-6 B、7.1×10^-7 C、1.4×10⁶ D、1.4×10⁷

查看试题解析
5. 下列计算正确的是（）

A、2a•3a=6a B、（﹣a³）²=a⁶ C、6a÷2a=3a D、（﹣2a）³=﹣6a³

查看试题解析
6. 如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，若添加下列一个条件后，仍然不能证明△ABC≌△DEF，则这个条件是（）

A、∠A＝∠D B、BC＝EF C、∠ACB＝∠F D、AC＝DF

查看试题解析
7. 已知△ABC的周长为m，BC=m-2AB，则下列直线一定为△ABC的对称轴的是（）

A、△ABC的边BC上的中线所在的直线 B、∠ACB的平分线所在的直线 C、△ABC的边AB的垂直平分线 D、△ABC的边AC上的高所在的直线

查看试题解析
8. 下列分式中，不是最简分式的是（）

A、 $\frac{x^{2} - 1}{x^{2} + 1}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{x^{2} - 1}{x}$ D、 $\frac{x - 1}{x + 1}$

查看试题解析
9. 下列运算错误的是（）

A、 $\frac{{(a - b)}^{2}}{{(b - a)}^{2}} = 1$ B、 $\frac{- a - b}{a + b} = - 1$ C、 $\frac{0.5 a + b}{0.2 a - 0.3 b} = \frac{5 a + 10 b}{2 a - 3 b}$ D、 $\frac{a - b}{a + b} = \frac{b - a}{b + a}$

查看试题解析
10. 如图所示，已知 $A B = A C$ ， $A D = A E$ ，要证 $△ A B D ≌ △ A C E$ ，需补充的条件是（）

A、 $∠ B = ∠ C$ B、 $∠ D = ∠ E$ C、 $∠ 1 = ∠ 2$ D、 $∠ C A D = ∠ D A C$

查看试题解析
11.
如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=3，则DE的长为（　　）

A、1 B、2 C、3 D、4

查看试题解析
12. 分式方程 $\frac{x}{x - 1} - 1 = \frac{m}{(x - 1) (x + 2)}$ 有增根，则m的值为（　　）

A、0和3 B、1 C、1和﹣2 D、3

查看试题解析

二、填空题

13. 已知一个多边形的内角和为540°，则这个多边形是边形．

查看试题解析
14. 计算：8x⁶÷4x²＝．

查看试题解析
15. 多项式x2+1添加一个单项式后可变为完全平方式，则添加的单项式可以是.(任写一个符合条件的即可)

查看试题解析
16. 若ab=2，a﹣b=﹣1，则代数式a²b﹣ab²的值等于．

查看试题解析
17. 若代数式 $\frac{6}{x + 2}$ 与 $\frac{4}{x}$ 的值相等，则x= ．

查看试题解析
18. 已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠AEB＝度．

查看试题解析
19. 已知10^m=2，10ⁿ=3，则10^3m+2n= ．

查看试题解析
20. $Δ A B C$ 中， $A B = A C$ ， $∠ A = 30^{\circ}$ ，点 $E$ 为 $B C$ 延长线上一点， $∠ A B C$ 与 $∠ A C E$ 的平分线相交于点 $D$ ，则 $∠ D$ 的度数为．

查看试题解析

三、解答题

21. 分解因式：

(1)、 $\frac{1}{3} x^{2} - 2 x + 3$ ；

(2)、 $16 - 8 {(x + y)}^{2} + {(x + y)}^{4}$ ．

查看试题解析
22. 先化简，再求值：
(a＋b)(a－b)－(a－2b)² ，其中a＝2，b＝－1.

查看试题解析
23. 如图，D是 $A B$ 上一点， $D F$ 交 $A C$ 于点E， $D E = E F$ ， $F C ∥ A B$ ，求证： $A E = C E$ ．

查看试题解析
24. 计算 $(\frac{m}{m - 2} - \frac{2 m}{m^{2} - 4}) \div \frac{m}{m + 2}$ ．

查看试题解析
25. 解方程： $\frac{2}{x + 1} = \frac{x}{x - 1} - 1$ ．

查看试题解析
26. 由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）。请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它沿着某条直线折叠后直线两旁的图形能完全重合.

查看试题解析
27. 甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的 $\frac{1}{2}$ ，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家出发去学校，结果甲同学比乙同学早到2分钟．

(1)、求乙骑自行车的速度；

(2)、当甲到达学校时，乙同学离学校还有多远？

查看试题解析
28. 如图

(1)、如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部，若∠A=30︒，则∠ABC+∠ACB=︒，∠XBC+∠XCB=︒

(2)、如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，直角顶点X还在△ABC内部，那么∠ABX+∠ACX的大小是否变化?若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小．

查看试题解析